Preuve Proof Prueba

Web Newsletter
Juillet/Août 1998

Nouveautés

News

Noticias

1998

Barbin E. (1998) La démonstration: pulsation entre le dicursif et le visuel. In: actes du colloque "Produire et lire des textes de démonstrations". Rennes: Université de Rennes et IREM, janvier 1998 (à paraître)
Grenier D., Payan C. (1998) Spécificité de la preuve et de la modélisation en mathématiques discrètes. Recherches en Didactique des Mathématiques 18(1) 59-100.
Hoyles C., Jones K. (1998), Proof in Dynamic Geometry Contexts. In: Mammana C., V. Villani V. (eds) Perspectives on the Teaching of Geometry for the 21st Century (pp.121-128) Dordrecht: Kluwer.
Luengo V., Balacheff N. (1998) Contraintes informatiques et environnements d'apprentissage de la démonstration en géométrie. Sciences et techniques éducatives 5(1) 15-45.
Ross K. A. (1998) Doing and Proving: The place of Algorithms and Proof in School Mathematics American Mathematical Monthly , 252-255.
Winsløw C. (1998) A linguistic approach to the justification problem in mathematics education. For the Learning of Mathematics 18(1) 10-16.

Archives

Barbin E. (1996) Historicité de la notion d'évidence en géométrie entre évidence visuelle et évidence manipulatoire. In: Proceedings Braga, Historìa Matematicà (vol.1). Universidade do Hinho
Beaulieu L. (1990) Proof in expository writing -- Some examples from Bourbaki's early drafts. Interchange 21(2) 35-45.

PME22 programme preview

Arzarello F. et al., A model for analysing the transition to formal proof in geometry.
Olivero F. et al., Dragging in Cabri and modalities transition from conjectures to proofs in geometry.
Baldino R., Dialectical proof: should we teach it to physics students.
Cifarelli V., Abductive inference: connections between problem posing and solving.
de Villiers M., To teach definition in geometry or to teach to define?
Gardiner J., The evolution of pupils' ideas of construction and proof using hand-held dynamic geometry technology.
Garuti R. et al., Cognitive unity of theorems and difficulty of proof.
Hadas N. et al., Proof in geometry as an explanatory and convincing tool.
Reid D. et al., Why is proof by contradiction difficult?
Rowland T., Conviction, explanation and generic examples.
Waring S. et al., An experiment in developing proof through pattern.
Yackel E. et al, A study of argumentation in a second-grade mathematics classroom.
Zaslavsky O. et al., Students'understanding of the role of counter-examples.

Learn more about next PME22 conference, connecting to: http://www.sun.ac.za/pme22/

Textes en ligne

Ross K. A. (1998) Doing and Proving: The place of Algorithms and Proof in School Mathematics
Garuti R., Boero P., Lemut E. (1998) Cognitive unity of theorems and difficulty of proof.
Grenier D., Payan C. (1998) Spécificité de la preuve et de la modélisation en mathématiques discrètes.

 

Français  The Theme of the Letter Proof and perception II by Michael Otte  Español The goal of the Theme of the Letter is the stimulation of exchanges on current questions about the learning and the teaching of mathematical proof. This new contribution of Michael Otte is a continuation of the text we published in the Janvier/Février 1998 issue of the Proof Newsletter.   From his analysis of empiricism in general and of Hume's skepticism in particular, Kant concluded that space (and time) are not objects, but conditions of perception. With regard to mathematics, this is expressed in the algebraization and axiomatization in Hilbert's terms. Hilbert himself refers to the analogy between algebra and axiomatics writing: "Intuitive, material number theory, as we have been construing it, does not include the method of algebraic computation with letters. Formulas were always used exclusively for communication in intuitive number theory. ... In algebra, on the other hand, we regard expressions containing letters as independent structures which formalize the material theorems of number theory. In place of statements about numerical symbols, we have formulas which are themselves the concrete objects of intuitive study. In place of number-theoretic material proof, we have the derivation of a formula form another formula according to determinate rules. Hence, as we see even in algebra, a proliferation of finitary objects take place" (D. Hilbert, On the Infinite, in: Philosophy of mathematics (ed. by P. Benacerraf & H. Putnam), Cambridge University Press, Cambridge 1964, 195). Mathematics as a form of relational thinking is not concerned with objects or their properties as such, and neither with relations between objects in themselves, but rather with relations between possible objects of activity. Any perception which does not focus on activity or its trajectories in space will lead to apories and paradoxes. This is visible, in particular, in the problematic of the infinite and of the continuum and conveys significance to what Piaget has called reflexive abstraction, and Peirce hypostatic abstraction, abstractions which make allowance for the processes of transforming activities themselves into cognitive objects or concepts. Mathematics, and in particular axiomatized mathematics, considers objects only with regard to the consequences they might have for the process of mathematical reasoning. Hence, mathematics is foremost concerned with the manner objects could be introduced into mathematical reasoning or theory. Mathematical objects are intensional objects in the first place, that is objects whose criteria of individuation are to be seen in the specific way they are introduced into theory (by means of definitions or constructions, for instance). Two mathematical objects can be extensionally identical, but intensionally different by being presented differently. The famous "x" of algebra which serves to introduce an unknown object into activity is one example for this. Just like other sciences, however, mathematics is interested in obtaining objective insights, and hence in extensional objects. This is why mathematical theorems or axioms as a rule have the form of equations A = B. Alongside with theory based principles of equality we need ostensive indications of particulars. Through language alone we could never come to know that something exists. In Frege's famous essay on "Sinn und Bedeutung", the author gives some examples from elementary geometry. Frege writes: "Let a, b, c be the lines connecting the vertices of a triangle with the midpoints of the opposite sides. The point of intersection of a and b is then the same as the point of intersection of b and c. So we have different designations for the same point and these names ("point of intersection of a and b"; "point of intersection of b and c") likewise indicate the mode of presentation and hence the statement contains actual knowledge. It is natural to think of there being connected with the sign besides that which the sign designates, which may be called the meaning (or reference) of the sign, also what I should like call the sense of the sign, wherein the mode of presentation is contained. In our example the meaning of the expressions "point of intersection of a and b" and "point of intersection of b and c" would be the same, but not their sense". How do I know, or how can I convey, that A and B designate the very same object? For this, space and the ostensive indication of points in space are important. A letter in geometry, like a variable in algebra, is an index, that implies a sort of existence claim concerning the object indicated but not presenting any characteristics of that object. These letters in geometry indicate places. There will always be different paths leading to the same place. And once we have arrived there, further paths and possibilities will always appear. This is the precise reason why it is critical to note those features of objects or concepts which will be subsequently needed in reasoning. Space in this way becomes the condition for the possibility of cognition, iconic representations of relationships as well as indices playing essential roles in this. In this context, I should like to present an example taken from "Cabri" computer geometry. Be given a triangle with the vertices 1, 2 and 3. Now one starts the following construction at an arbitrary point G, constructing first the point E which is symmetrical to G with regard to the vertex 1, then the point F which is symmetrical to E with respect to 2, and finally the point Z which is symmetrical to F with regard to 3. Now the midpoint of the line segment GZ is marked. The "Cabri" system permits to pull or move points and lines across the monitor. If the initial point G is moved on the monitor, it is surprising to see that the midpoint M of the line segment GZ remains fixed despite the fact that its definition resp. construction obviously depends on G and thus ought to vary along with G. This means that there must be a different form N of presenting the respective referent, a form which is independent of the point G. And the fact of the invariance of the midpoint may then be expressed by the equation M = N. 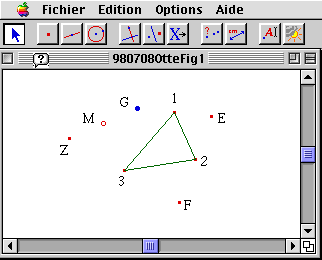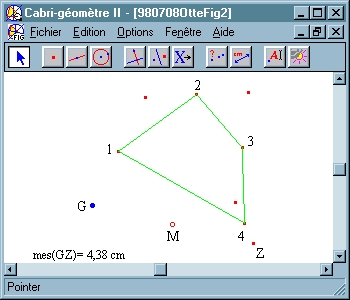If we now repeat the same procedure with regard to an initial constellation of 4 or 6 points, or more general of (2n) points, we do not encounter any fixed point, but rather observe that the distance between the initial point G and the end point Z remains invariant. While we may select the point G, in the case of the triangle or of any odd number of initial points, such as to close the broken line drawn from G across the symmetrical points to Z, or in other terms to make G and Z coincide, and thus turn the initial constellation of the points 1, 2, 3 into a system of side midpoints of a (non-necessarily convex) polygon, this is not the case for an even number of initial points. Whether the first and end points of the construction will coincide here depends exclusively on the constellation of the initially selected points 1, 2, 3, 4. In the case of 4 vertices, these will have to form a parallelogram, for instance. This is a fact well-known from school geometry which also explains the triangle situation, for the further determination of the midpoint I have represented by N simply consists in selecting this point such as to complete the vertices 1, 2, 3 of the initial triangle into a parallelogram. It may now be asked which condition 2n points must satisfy in order to form a system of midpoints belonging to a polygon. Every regular hexagon can obviously be included within another regular hexagon in such a way that its corners are precisely the side midpoints of the larger hexagon. The entire constellation, however, is immediately destroyed by pulling even a little bit only on any vertex of the hexagon. It is possible to conduct ever new experiments of this kind, "Cabri" permitting both to construct and to vary constructions in a very simple way and offering rich possibilities for inductive reasoning. But even after an entire week of experimenting, neither the teachers nor the students had came across any hypothesis concerning the constellation of 6 points which adequately generalizes the parallelogram condition for the case of the quadrangle, the monitor only showing the constructions in their results. All the objects appear like empirical objects of perception and nobody was able to offer an inductive hypothesis. In the given situation, algebra now re-establishes the connection between object and activity. What distinguishes algebraic calculation from observing an situation in itself? Algebra shows something different from the fact in itself, that is a point's invariance or the invariance of the distance between the initial point and the end point of the even numbered n-polygon. Algebra shows a relational fact, because it maps activity itself. And mathematics, as has been said, has to do with relations between object-related activities. Everything general becomes effective only via activity. Even a natural law will not apply itself. A stone will drop only if I let it fall, and only then will I be able to perceive the law of gravity. Only as soon as we actively reflect on the conditions of the experiment of falling bodies, however, rather than just observe them as they are falling down, may we hope to find the form of the law. This shift of viewpoint is in mathematics accomplished by algebraization, algebra being the activity and method of formal construction. To make matters concrete, let us begin in the present case of any even number of initial points by applying vector calculus, i.e. by using linear algebra to obtain the conditions which the coordinates of the initial points must satisfy. After some calculation, it is easily seen that the sums of coordinates of the points with even numeration, that is 2, 4, 6 ... etc. must be equal to the sums of the coordinates of the points with odd numeration, that is 1, 3, 5 ... etc. In geometrico-physical interpretation, this means that the centers of gravity of the even-numbered points constellation and of the odd-numbered one will coincide. In the case of n=6, this means that the triangle 1, 3, 5 has the same center of gravity as the triangle 2, 4, 6. This now seems to be an entirely contingent fact, and there are no higher grounds which make the fact predictable or might represent how it evolved. The conditions of the result have simply been calculated. Knowledge will always refer to things factual as long as I do not know the conditions of possibility of this knowledge. In the case of algebra, however, this fact is of a nature different from that of empirical observation. It is indeed a relational fact for it co-represents, as has been said, activity itself. In calculating, I have done nothing but map the geometrico-empirical process of construction quite verbally into a vectorial-algebraic mode. In order to arrive at any kind of insight or meaning, I must now return to the geometrico-intuitive level and to the semantic resources it offers. Why do the center of gravity of the two triangles coincide in the case of n=6? Quite simply because they are nothing but different intensions of the same extension, or in other terms, because they represent different modes of representing the overall center of gravity. This is true, as has been said, only if the system of the original 6 points is a system of side midpoints belonging to another, larger hexagonal polygon. If we assume that the points of this hexagonal polygon represent a distribution of mass, and if we want to determine this mass distribution's center of gravity, we may do this in different ways. We may select the points 1, 3, 5. Each of these points represents as midpoint the center of gravity of the two corners of the respective side. That is, the point system 1, 3, 5 replaces the original system of 6 points and is again replaced by the 1, 3, 5 triangle's center of gravity. We may now carry out the same procedure of determining the center of gravity for the initial constellation of six points with regard to the points 2, 4, 6, having of course to arrive at the same overall center of gravity. In other words: the 6 points 1, 2, 3 ... represent a system of midpoints of a hexagonal polygon only if the center of gravity of the two triangles 1, 3, 5 and 2, 4, 6 are nothing but two different ways of determining one and the same point, that is if they are two intensionally different and extensionally identical objects. This is quite easily observable in the case of the quadrangle. In this case, I may replace the 4 points, for example, by the two midpoints 1 and 3, and these midpoints again by the midpoint of their connecting line. We can do the same with midpoints 2 and 4. Now we are able to understand why the midpoint quadrangle within any quadrangle must needs be a parallelogram: diagonal lines will halve one another only within the parallelogram. It has been claimed over and again that the so-called context of discovery has to be separated from the contexts of justification as well as that mathematical proof belongs exclusively to the latter. But the idea of formal proof arose together with algebraization (see for instance I. Hacking, Leibniz and Descartes: Proof and Eternal Truths, in: Philosophy through its Past, Penguin Books 1984) and thus implies the transition from thinking in objects to relational thinking. Proof thus is linked with mathematical generalization, which takes mathematical functions or operations as its starting point rather than objective constellations as such. Vector calculus, for instance, essentially presupposes a generalization of multiplication omitting commutativity (it came about when people like Grassmann tried to apply the form of Newton's law of gravitational interaction on electrodynamical attraction). Mathematics advances by means of an interplay of formal construction and perception or observation and proof is embedded into this dialectics.   Reaction? Remarks? Reactions to Otte's contribution will be published in the September/October issue of the Proof Newsletter 1998 © Michael Otte 1998

BSRLM Geometry Working Group The BSRLM Geometry Working Group met at the University of Birmingham (UK) on Saturday June 20th. Currently the group is examining the nature of geometrical reasoning, focusing on aspects of a framework proposed by the French psychologist Raymond Duval.    Duval has suggested that geometrical reasoning involves three kinds of cognitive processes which fulfill specific epistemological functions: visualisation processes (including, for example the illustration of a geometrical statement, heuristic exploration of a complex situation, subjective verification) construction processes (using tools) reasoning processes (particularly discursive processes for the extension of knowledge, for proof, for explanation) Duval's view is that these different processes can be performed separately, but that these three kinds of cognitive processes are closely connected and their "synergy is cognitively necessary for proficiency in geometry". At the meeting of the working group, Kev Delaney (of Nottingham Trent University) initiated a discussion of visualisation processes, asking whether visualisation takes different forms, and what these forms might be. All contributions to this discussion are welcome. The group is open to all. ADVANCE NOTICE The fourth British Congress on Mathematical Education The fourth British Congress on Mathematical Education takes place on 15-17 July, 1999 at Nene College in Northamptonshire (UK). The programme will include a discussion on the teaching and learning of geometry, organised by Keith Jones (University of Southampton) and Dave Hewitt (University of Birmingham). Offers of contributions to the discussion are invited, including any from colleagues from outside the UK who might be in Britain at that time. Keith Jones University of Southampton Research and Graduate School of Education Highfield Southampton SO17 1BJ UK The MAA and the NCTM Standards The Ross's paper reproduced here online with the authorization of The American Mathematical Monthly is a subset of the entire MAA website which reports on the interaction of the MAA with NCTM concerning the NCTM Standards. The first part is a brief history of the interaction up to 1996. Since many people want to know just what the MAA's first "endorsement" was about, the report begins with the relevant minutes of the January 1989 meeting of the MAA Board of Governors. This is followed by commentary from the agenda of that meeting. Events leading up to the formation of the MAA President's Task Force on the MAA Standards, its charge and its membership are given. Its primary charge is to respond to questions and issues posed by the NCTM Commission on the Future of the Standards. To learn more connect to:

Xième Ecole d'été de Didactique des Mathématiques 15-18 août 1999 Houlgate - France   Parmi les thèmes qui seront abordés lors de cette Ecole on annonce : Preuves, démonstrations et écritures en mathématiques L'Ecole d'été de didactique des mathématiques est un lieu de formation des chercheurs. Cette Ecole contribue ainsi de manière essentielle à l'actualisation du corpus des connaissances sur lequel reposent les enseignements universitaires de didactique des mathématiques, et offre également des matériaux et des pistes de réflexion pour la formation des enseignants. J.B. Lagrange 5 rue Yves Montand FR-35590 St GILLES France Mettre en en-tête du courrier électonique : " EE ddm 10"   THE MATH FORUM INTERNET NEWS 18 May 1998, Vol.3, No.20   http://forum.swarthmore.edu/electronic.newsletter/   EUCLID'S ELEMENTS David Joyce "Euclid's Elements form one of the most beautiful and influential works of science in the history of humankind. Its beauty lies in its logical development of geometry and other branches of mathematics. It has influenced all branches of science but none so much as mathematics and the exact sciences. The Elements have been studied [for] 24 centuries in many languages starting, of course, in the original Greek, then in Arabic, Latin, and many modern languages." David Joyce created these Web pages to rekindle an interest in the Elements, and to show how Java applets can be used to illustrate geometry. The text of all 13 Books is complete, and all of the figures are illustrated using the "Geometry Applet," including those that are three-dimensional, found in the last three books on solid geometry. References to Euclid's Elements on the Web are included. http://aleph0.clarku.edu/~djoyce/java/elements/elements.html EUCLID'S GEOMETRY: HISTORY AND PRACTICE Alex Pearson A series of interdisciplinary lessons on Euclid's Elements, researched and written by Alex Pearson, a Classicist at The Episcopal Academy in Merion, Pennsylvania. The material is organized into class work, short historical articles, assignments, essay questions, and a quiz. http://forum.swarthmore.edu/geometry/wwweuclid/

Services La bibliographie Outil de recherche Cours en ligne Questions et réponses A propos du site

Services The bibliography Search tool Online course Questions and answers About the site

Servicios La bibliografia Herramienta de busqueda Curso electronico Preguntas y repuestas Con respecto a este servidor