|
|
|
El Tema de la Gacetilla tiene se propone estimular conversaciones acerca de cuestiones vigentes en el aprendizaje y la enseñanza de la prueba en matemática. Esta nueva contribución de Michael Otte es una continuación del texto que fuera publicado en la edición de Enero/Febrero 1998 de esta Gacetilla sobre la Prueba. A partir de su análisis del empirismo en general y del escepticismo de Hume en particular, Kant llegó a la conclusion de que el espacio y el tiempo no son objetos sino condiciones de la percepción. Para la matemática, la expresión de aquella conclusión está presente en la algebrización y la axiomatización que siguen las ideas de Hilbert. Hilbert mismo se refiere a la analogía entre el álgebra y la axiomática cuando escribe
La matemática, como una forma de pensamiento relacional, no se ocupa de objetos o de sus propiedades como tales. La matemática tampoco se ocupa de las relaciones entre los objetos por sí mismos. La matemática se ocupa de las relaciones entre los posibles objetos de actividad. Cualquier percepción que no se ocupe de la actividad y de sus trayectorias en el espacio conduce a aporías y paradojas. Esto es visible, en particular, en la problemática del infinito y del contínuo, y confiere sentido a lo que Piaget llama abstracción reflexiva y a lo que Peirce llama abstracción hypostáticaæabstracciones que permiten los procesos de transformación de las actividades mismas en conceptos u objetos cognitivos. La matemática, y en particular la matemática axiomatizada, considera a los objetos solamente en lo que tiene que ver con las consecuencias que estos objetos puedan tener en los procesos de razonamiento matemático. Es decir, la matemática se ocupa fundamentalmente de la manera según la cual se pueden introducir objetos en el razonamiento matemático o en la teoría. Los objetos matemáticos son, en primer lugar, intensionales, es decir, objetos cuyos criterios de distinción se manifiestan en la forma específica en la que son introducidos a la teoría (por medio de definiciones o construcciones, por ejemplo). Dos objetos matemáticos pueden ser idénticos en su extensión, pero diferentes en su intensión por haber sido presentados de forma diferente. La famosa "x" del álgebra, que sirve para introducir un objeto desconocido a la actividad es un ejemplo de aquéllo. Tal como otras ciencias, sin embargo, la matemática se interesa en producir intuiciones objetivas, por lo tanto objetos extensionales. Ésa es la razón por la cual en general los teoremas matemáticos o los axiomas tienen la forma de una ecuación A = B. Además de una teoría basada en los principios de igualdad, se necesitan indicaciones ostensivas de los particulares. A través del lenguaje solamente uno jamás podría llegar a saber que algo existe. En el famoso ensayo de Frege "Sinn und Bedeutung," el autor proporciona algunos ejemplos de la geometría elemental. Frege dice:
¿Cómo sé yo, o cómo puedo transmitir el hecho de que A y B designen el mismo objeto? Para ésto, el espacio y la indicación ostensiva de puntos en el espacio son importantes. Una letra en geometría, tal como una variable en álgebra, es un índice que implica una suerte de afirmación de existencia con respecto al objeto indicado pero que no presenta ninguna de las características de ése objeto. Esas letras en geometría indican lugares. Siempre hay diferentes caminos que llevan al mismo lugar. Y una vez que uno llega a ese lugar, aún otros caminos y posibilidades aparecen incesantemente. Ésta es la precisa razón por la cual es imprescindible notar aquellas características de objetos o conceptos que serán necesarias subsecuentemente en el razonamiento. El espacio de esta manera se convierte en la condición de posibilidad para la cognición; y la representación icónica de relaciones y los índices tienen un papel esencial en ésto.
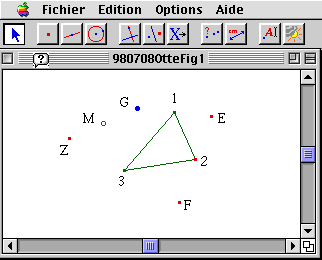
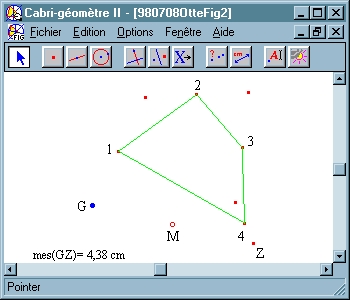
Si bien para el caso del triángulo, o para un conjunto impar de puntos iniciales, uno puede elegir el punto G de tal suerte que se cierre la línea quebrada trazada a través de los puntos simétricos hasta Z, o en otras palabras hacer que G y Z coincidan y por lo tanto convertir la constelación inicial de puntos 1, 2, 3 en un sistema de puntos medios de los lados de un polígono (no necesariamente convexo), no es así cuando el número inicial de puntos es par. La posibilidad de que los puntos inicial y final de la construcción coincidan, depende aquí exclusivamente de la constelación de puntos elegidos inicialmente 1, 2, 3, 4. En el caso de 4 vértices, por ejemplo, estos formarán un paralelogramo. Este es un hecho bien conocido de la geometría escolar que también sirve para explicar la situación del triángulo, dado que la segunda determinación del punto medio a la que he denotado como N consiste simplemente en elegir este punto de tal manera que complete los vértices 1, 2, y 3 del triángulo inicial para determinar un paralelogramo.
En la situación dada, el álgebra puede reestablecer la conexión entre el objeto y la actividad. ¿Qué distingue el cálculo algebraico de la observación de una situación en sí misma? El álgebra muestra algo diferente de los hechos mismos, los cuales son la invarianza de un punto o de la distancia entre el punto inicial y el punto final en el polígono de un número par de lados. El álgebra muestra un hecho relacional, pues proyecta la actividad en sí misma. Y la matemática, como se ha dicho, tiene que ver con relaciones entre actividades relacionadas con los objetos. Cualquier cosa general se vuelve efectiva solamente a través de la actividad. Ni siquiera una ley natural se aplicará por sí misma. Una piedra caerá solamente si yo la dejo caer, y solamente así podré percibir la ley de la gravedad. Solamente cuando reflexionamos activamente sobre las condiciones del experimento de caída libre de los cuerpos, sin embargo, en lugar de solamente observarlos cuando caen, podemos tener la esperanza de encontrar la forma de la ley. Este cambio de punto de vista se realiza en matemática mediante la algebrización, donde el álgebra es la actividad y el método de construcción formal. Para concretar, comencemos, en el caso de cualquier número par de puntos iniciales, mediante aplicar cálculo de vectores, es decir, usando álgebra lineal para obtener las condiciones que deben satisfacer las coordenadas de los puntos iniciales. Luego de algunos cálculos, se ve fácilmente que las sumas de las coordenadas de los puntos numerados par, es decir los puntos 2, 4, 6, etc. deben ser iguales a las sumas de las coordenadas de los puntos numerados impar, es decir los puntos 1, 3, 5, etc. En una interpretación físico-geométrica, aquello quiere decir que los centros de gravedad de las constelaciones de puntos numeradas par e impar respectivamente, deben coincidir. En el caso de n = 6 esto quiere decir que el triángulo 1, 3, 5 tiene el mismo centro de gravedad que el triángulo 2, 4, 6. Esto parece ser un hecho completamente contingente, y no hay elementos disponibles que permitan mostrar que el hecho es predecible, ni siquiera que permitan representar cómo ha evolucionado. Las condiciones del resultado han sido simplemente calculadas. El conocimiento se referirá siempre a los hechos si yo sigo sin conocer las condiciones de posibilidad de este conocimiento. En el caso del álgebra, no obstante, este hecho es de una naturaleza diferente del de la observación empírica. Se trata en realidad de un hecho relacional porque co-representa, tal como se ha dicho, la actividad en sí misma. Al calcular, no he hecho otra cosa sino proyectar verbalmente el proceso geométrico-empírico de construcción en un modo vectorial-algebraico. Para aprehender cualquier intuición o sentido, debo volver al nivel geométrico-intuitivo y a los recursos semánticos que este nivel ofrece. ¿Por qué coinciden los centros de gravedad de los dos triángulos en el caso n= 6? Simplemente porque no son otra cosa sino intensiones diferentes de la misma extensión, o en otras palabras, porque constituyen modos distintos de representar el centro de gravedad del conjunto. Esto es verdad, como se ha dicho, solamente si el sistema original de 6 puntos es un sistema de puntos medios de los lados de otro hexágono, más grande. Si asumimos que los puntos de este hexágono representan una distribución de masa, y si queremos determinar el centro de gravedad de esta distribución de masa, esto se puede hacer de varias maneras. Podemos elegir los puntos 1, 3, 5. Cada uno de esos puntos representa, en tanto punto medio, el centro de gravedad de dos vértices del lado respectivo. Es decir, el sistema de puntos 1, 3, 5 reemplaza el sistema original de 6 puntos y es reemplazado a su vez por el centro de gravedad del triangulo 1, 3, 5. Podemos ahora ejecutar el mismo procedimiento para determinar el centro de gravedad de la constelación inicial de seis puntos con respecto a los puntos 2, 4, 6 obteniendo así, por supuesto, el mismo centro de gravedad para el conjunto. En otras palabras: los 6 puntos 1, 2, 3, Š representan un sistema de puntos medios de un hexágono solamente si el centro de gravedad de los dos triángulos 1, 3, 5 y 2, 4, 6 no son otra cosa sino dos maneras diferentes de determinar un solo punto, es decir dos objetos diferentes en intensión e idénticos en extensión. Esto se observa fácilmente en el caso del cuadrángulo. En este caso, puedo reemplazar los cuatro puntos, por ejemplo, por dos puntos medios 1 y 3, y esos puntos medios nuevamente por el punto medio del segmento que los une. Podemos hacer lo mismo con los puntos medios 2 y 4. Ahora uno puede entender por qué el cuadrángulo formado por los puntos medios de los lados de cualquier cuadrángulo es necesariamente un paralelogramo: Las diagonales se cortarán en su punto medio solamente en un paralelogramo. Se ha dicho varias veces que el así llamado contexto de descubrimiento es distinto de los contextos de justificación; se ha afirmado tambien que la demostración matemática solamente pertenece al segundo grupo. Pero la idea de prueba formal surgió conjuntamente con la algebrización (véase por ejemplo I. Hacking, Leibniz and Decartes: Proof and Proof and Eternal Truths, in: Philosophy through its Past, Penguin Books 1984) y por lo tanto implica la transición del pensamiento en términos de objetos al pensamiento relacional. La demostración se conecta entonces con la generalización matemática, que toma funciones u operaciones matemáticas como puntos de partida en lugar de constelaciones de objetos como tales. El cálculo vectorial, por ejemplo, esencialmente presupone una generalización de la multiplicación omitiendo la conmutatividad (apareció cuando Grassmann y otros intentaron aplicar la forma de la ley de interacción gravitatoria de Newton a la atracción electrodinámica). La matemática avanza mediante un interjuego entre construcción formal y percepción u observación, y la demostración o la prueba forman parte de ésta dialéctica. |