|
|
|
Le thème de la Lettre a pour but de stimuler des échanges autour de quelques questions d'actualité sur l'apprentissage et l'enseignement de la démonstration en mathématiques. Cette nouvelle contribution de Michael Otte est une suite du texte publié dans la Lettre de la Preuve de Janvier/Février 1998 .
De son analyse de l'empirisme en général et du scepticisme de Hume en particulier, Kant conclut que l'espace (et le temps) ne sont pas des objets mais des conditions de la perception. En ce qui concerne les mathématiques ceci est exprimé par l'algébrisation et l'axiomatisation au sens de Hilbert. Hilbert lui-même renvoie à l'analogie entre l'algèbre et l'axiomatisation lorsqu'il écrit :
Comme forme de pensée rationnelle, les mathématiques ne sont pas concernées par les objets ou leurs propriétés en tant que tels, ni même par les relations entre les objets pour elle-mêmes, mais plutôt par les relations entre les objets potentiels de l'activité. Toute perception qui ne se centre pas sur l'activité ou ses trajectoires dans l'espace conduira à des apories ou des paradoxes. Ceci est visible, en particulier, dans la problématique de l'infini et du continu, et donne une signification à ce que Piaget a appelé l'abstraction réfléchissante, et Peirce l'abstraction hypostatique -- abstractions qui permettent la transformation des activités en des objets de la cognition ou des concepts. Les mathématiques, et en particulier les mathématiques axiomatiques, considèrent les objets uniquement du point de vue de l'impact qu'ils pourraient avoir sur le raisonnement mathématique. Ainsi, les mathématiques sont avant tout concernées par la façon dont les objets pourraient être introduits dans le raisonnement mathématique ou dans la théorie. Les objets mathématiques sont d'abord des objets intentionnels, c'est-à-dire des objets dont le critère de singularité doit être recherché dans la façon spécifique dont ils sont introduits dans la théorie (par le moyen de définitions ou de constructions, par exemple). Deux objets mathématiques peuvent être identiques en extension, mais être différents en intention parce qu'ils ont été présentés de façons différentes. Le fameux "x" de l'algèbre qui sert à introduire un objet inconnu dans l'activité en est un exemple. Comme d'autres sciences, cependant, les mathématiques sont intéressées à développer une intuition objective, et donc intéressées par les objets "extensionnels". C'est pourquoi les théorèmes mathématiques et les axiomes, en tant que règles, ont la forme d'équations du type A=B. Avec les principes d'égalité fondés théoriquement, nous avons besoin du soutien ostensif d'entités particulières. Par le langage seul nous ne pourrions jamais découvrir que quelque chose existe. Dans l'essai fameux de Frege, "Sinn und Bedeutung", l'auteur en donne quelques exemples tirés de la géométrie élémentaire. Frege écrit :
Ces lettres, en géométrie, indiquent des lieux. Il y aura toujours des voies différentes conduisant au même lieu. Et une fois arrivé au but, d'autres voies et d'autres possibilités apparaitront toujours. C'est précisément pour cette raison qu'il est crucial d'identifier les aspects des objets ou des concepts qui seront ensuite nécessaires au raisonnement. L'espace, de cette façon, devient la condition de la cognition, les représentations iconiques des relations, comme indices, jouent ici un rôle essentiel.
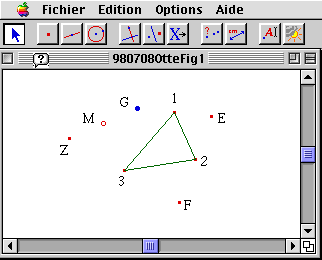
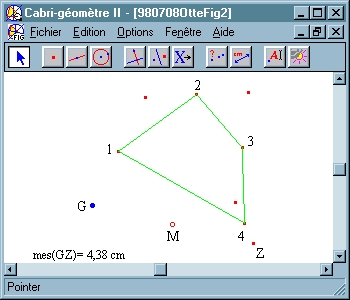
Si, maintenant, on reproduit la même procédure avec une configuration initiale de 4 ou 6 points, ou plus généralement (2n) points, on ne remarque aucun point fixe, en revanche on observe que la distance entre le point initial G et le point final Z reste constante. Alors que l'on peut positionner le point G, dans le cas du triangle ou de toute configuration d'un nombre impair de points, de façon à fermer la ligne brisée GZ constituée des images symétriques, en d'autres termes faire coïncider G et Z, et donc transformer la configuration initiale de points 1, 2, 3 en un système de points milieux d'un polygone (non nécessairement convexe), cela n'est pas le cas pour un nombre pair de points initiaux. La coïncidence du point initial et final de la construction dépend dans ce cas seulement de configuration initiale des points 1, 2, 3, 4 choisie. Dans le cas de 4 sommets, par exemple, ils formeront un parallélogramme. C'est en fait un résultat connu de géométrie élémentaire scolaire, qui explique aussi le cas du triangle, dans la mesure où l'interêt pour le point milieu que j'ai appelé N plus haut tient simplement à ce qu'il complète l'ensemble des sommets du triangle initial 1, 2, 3 pour obtenir un parallélogramme.
Dans cette situation, l'algèbre restaure la relation entre objet et activité. Qu'est-ce qui distingue le calcul algébrique de l'observation d'une situation ? L'algèbre montre quelque chose de différent du fait lui-même, c'est à dire l'invariance de point ou l'invariance de la distance entre le point initial et final dans le cas d'un polygone ayant un nombre pair de sommets. L'algèbre montre une relation parce qu'elle rend compte de l'activité elle-même. Et les mathématiques, comme je l'ai dit plus haut, concerne les relations entre les activités associées aux objets. Les choses ne deviennent effectives que par le biais de l'activité. Même une loi naturelle ne s'applique pas elle-même. Une pierre ne tombe que si on la fait tomber, et seulement dans ce cas on peut observer la loi de la gravité. D'ailleurs, ce n'est que lorsqu'on réfléchit activement sur les conditions expérimentales de la chute des corps plutôt que de seulement les observer lorsqu'ils tombent, que l'on peut espérer trouver l'expression de cette loi. Ce déplacement de point de vue est réalisé en mathématiques par l'algébrisation, l'agèbre étant l'activité et la méthode de construction formelle. Pour rendre les choses concrètes, commençons par le cas d'un nombre pair quelconque de points initiaux en appliquant le calcul vectoriel, i.e. en utilisant l'algèbre linéaire pour obtenir les conditions que doivent satisfaire les coordonnées des points initaux. Après quelques calculs, on peut voir aisément que la somme des coordonnées d'une famille de points pairs, c'est à dire 2, 4, 6, etc. doit être égale à la somme des coordonnées des points dans le cas impair, c'est à dire 1, 3, 5, etc. Dans une interprétation de géométrie physique, cela signifie que le centre de gravité d'un système pair de points et d'un système impair de points doivent coïncider Dans le cas n=6 cela signifie que le triangle 1, 3, 5 a le même centre de gravité que le triangle 2, 4, 6. Ceci semble être un fait totalement contingent, et il n'y a pas de meilleur fondement pour rendre le fait prédictible ou qui pourrait montrer comment il évolue. Les conditions du résultat ont simplement été calculées. La connaissance renverra toujours à des faits tant qu'on ne connait pas les conditions de possibilité de cette connaissance. Dans le cas de l'algèbre, cependant, ce fait est d'une nature différente de celle de l'observation empirique. C'est, bien sûr, un fait relationnel dans la mesure où il co-représente, comme je l'ai écrit, l'activité elle-même. En calculant, je n'ai rien fait de plus que d'associer, de façon assez littérale, le processus géométrique et empirique de construction à un mode algébrico-vectoriel. Pour parvenir à une quelconque compréhension ou intuition, je dois revenir maintenant au niveau intuitif et géométrique et aux ressources sémantiques qu'il offre. Pourquoi les centres de gravité de deux triangles coïncident dans le cas n=6 ? Tout simplement parce qu'ils ne sont rien d'autre que deux intentions difféntes de la même extension, ou en d'autres termes, parce qu'ils représentent différents modes de représentation du même centre de gravité. Ceci est vrai, comme je l'ai écrit, seulement dans le cas où le système original de 6 points est un système de points milieux d'un hexagone plus grand. Si l'on suppose que les points de cet hexagone représentent une distribution de masses, et si on veut déterminer le centre de gravité de cette distribution, on peut s'y prendre de différentes façons. On peut sélectionner les points 1, 3, 5. Chacun de ces points, en tant que milieu, représentant les centres de gravité des sommets des côtés correspondants. C'est-à-dire, le système de point 1, 3, 5 remplace le système original de 6 points et est remplacé à son tour par le centre de gravité du triangle 1, 3, 5. On peut maintenant réaliser la même procédure pour déterminer le centre de gravité de la configuration initiale des 6 points en considérant les points 2, 4, 6 pour arriver, évidemment, au même centre de gravité global. En d'autres termes: les 6 points 1, 2, 3 ... représentent un système de points milieux d'un hexagone seulement si les centres de gravité des deux triangles 1, 3, 5 et 2, 4, 6 ne sont pas autre chose que deux façons différentes de déterminer un même point, c'est à dire s'ils sont deux objets intentionnellement différents et extensionnellement identiques. Ceci est assez facile à observer dans le cas du quadrilatère. Dans ce cas, je pourrais remplacer les 4 points, par exemple, par les deux milieux 1 et 3, et ces milieux à leur tour par le milieu du bi-point qu'ils forment. On peut réaliser la même chose pour les points 2 et 4. On est alors en mesure de comprendre pourquoi le quadrilatère des milieux de tout quadrilatère est nécessairement un parallélogramme : les diagonales ne se coupent en leur milieu que dans le cas du parallélogramme. Il a été déclaré, ici et là, que le prétendu contexte de découverte devrait être séparé des contextes de justification et encore que la démonstration appartient exclusivement à ce dernier. Mais l'idée de preuve formelle est apparue avec l'algébrisation (voir par exemple à ce sujet : I. Hacking, Leibniz and Descartes: Proof and Eternal Truths, in: Philosophy through its Past, Penguin Books 1984) et donc implique le passage d'une pensée centrée sur les objets à une pensée centrée sur les relations. La démonstration est ainsi liée à la généralisation mathématique qui prend pour point de départ les fonctions mathématiques et les opérations plutôt que des configurations objectives en tant que telles. Le calcul vectoriel, par exemple, présuppose essentiellement une généralisation de la multiplication laissant de côté la commutativité (ceci est survenu lorsque des gens comme Grassmann ont essayé d'appliquer la forme de la loi sur l'interaction gravitationnelle de Newton à l'attraction électrodynamique). Les mathématiques avancent par le moyen d'un jeu entre construction formelle et perception ou observation, et la démonstation est prise dans cette dialectique.
publiées dans la Lettre de la Preuve de Septembre/Octobre |