La percepción y la Prueba III

Problema 1

Nuestro primer problema está tomado del libro de S. Papert, "Mindstorms" (Basic Books,1980, 146):

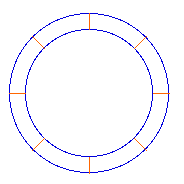
"Imagine una cuerda alrededor del globo terrestre, al que para este propósito lo consideraremos una esfera perfecta de cuatro mil millas de radio. Alguien propone sostener la cuerda de postes cuya altura es seis pies.    Obviamente esto implica que la cuerda deberá ser más larga. Surge una discusión acerca de cuánto más larga debería de ser la cuerda.    La mayoría de la gente que ha pasado por la escuela secundaria sabe como calcular la respuesta. Pero antes de hacerlo o de continuar la lectura trate de adivinar: Es aproximadamente mil millas mas larga, cien, o diez?" Papert luego sugiere que se busque una versión similar pero más simple: "Una buena regla general para simplificar es buscar una versión lineal. Por consiguiente propnemos el mismo problema asumiendo que la tierra es cuadrada."

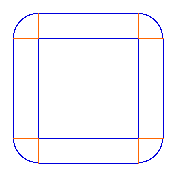
Si se aumenta el tamaño del cuadrado no se cambia las esquinas (de un cuarto de círculo cada una), de modo que el trozo de cuerda que falta para levantar la cuerda del suelo a una altura h es la misma para una tierra cuadrada muy pequenia o para una muy grande. Esto resuelve el problema.    La cantidad de cuerda que se necesita es 2ph. Papert mismo dice que el propósito de este problema no es "obtener la respuesta correcta," sino "buscar sensitivamente un conflicto entre distintas formas de pensar acerca del problema."

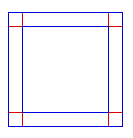
De una forma diferente y tal vez de modo más consistente, Leibniz podria sugerir una versión lineal.

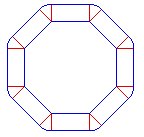
Pero Papert prefiere continuar así:

Sin embargo, ambos podrían apuntar al hecho de que su idea muestra que el tamaño de la "tierra" no importa a la hora de decidir cuánta cuerda extra se necesita. Esto finalmente resuelve el problema. De modo que ambas ideas, llamémoslas Cur (la idea de curvatura) y Lin (la idea de linealidad) respectivamente, aparecen como equivalentes con respecto al problema en cuestión.

Mueva el punto verde

Pero ambas ideas conducen a más. Tomemos la versión de Leibniz y para cada polígono regular (cuadrado, octógono, …) llamemos radio del polígono a la mínima distancia desde el centro hasta la frontera. Si se aumenta el radio en h se aumenta el perímetro en "el perímetro de un polígono semejante de radio h." Esto es exactamente la linealidad de la función representada representada por la forma geométrica misma. El todo es la suma de sus partes: Si el radio crece de x a (x + h) el perímetro aumenta de f(x) a f(x) + f(h). Por lo tanto tenemos que : f(x+h) = f(x) + f(h) and f(o) = o. El perímetro de un polígono es una función linea de su radio. Y el principio de continuidad implica el mismo resultado para el círculo (recuérdese que Leibniz fue el primero que empleó sistemáticamente este principio). Lo importante es que uno puede leer este hecho directamente de las figuras geométricas.

Uno puede ver con sus propios ojos que el alargamiento del perímetro está representado por un polígono de la misma forma. Para deducir otra representación de la función lineal, esta vez más constructiva que descriptiva, Leibniz haría notar que la forma del polígono no se cambia cuando la cuerda se tiende sobre postes (es decir, alargando el radio en h).

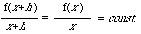y  y = f(x) = c.x

Los dos argumentos ilustran la idea de una conceptualización basada en una forma (formbased ).

La potencia de la idea Cur de Papert solamente puede apreciarse tan pronto como uno considera la expresión algebraica y = cx como la nueva forma pertinente. A diferencia del caso de Leibniz ahora obtenemos la misma función lineal y =2p x para todos los tipos de "globos terrestres" (de hecho el perímetro puede ser cualquier curva cerrada diferenciable a trozos que no se intersecte a sí misma). El factor de proporcionalidad 1(2p) da el número total de giros completos por los que pasan los postes cuando siguen la curva. Por lo tanto valores alternativos de c serían (n(2p) para n cualquier número entero; y de lo discreto del rango se entiende inmediatamente que pequeñas deformaciones en la curva no pueden cambiar el valor de c. El objecto geométrico en cuestión ya no es la curva sino un campo vectorial con respecto a la curva. El índice no cambia mientras las deformaciones de la curva no pasen por un cero del campo vectorial.
   De ésto se deriva un argumento fácil de entender con el que se justifica el teorema del punto fijo de Brouwer.

Ambas aproximaciones resuelven el problema 1 y desde este punto de vista aparecen como equivalentes. Presentamos ahora un segundo problema con respecto al cual las ideas Cur y Lin se demuestran no equivalentes. Este problema (sobre la epicicloide) se toma del libro de Robert Davis, "Learning Mathematics" (Croom Helm, London 1984, 216pp.).

Problema 2

"En un test reciente del ETS, una pregunta trataba de un círculo pequeño que rueda, sin deslizarse, alrededor de la circunferencia de un círculo más grande. (Puede pensarselos, si se quiere, como si fueran engranajes.) El radio del círculo grande es tres veces el radio del círculo pequeño…. Cuántas veces vemos rodar al círculo pequeño …."
  
Mueva el punto verde

Bob Davis continúa:

"Los expertos aparentemente razonaron esencialmente como sigue: Si el radio del círculo más grande es tres veces más grande, entonces el perímetro es tres veces más grande. 'Hacer rodar sin deslizar' quiere decir que las longitudes de arco son iguales. Como la longitud de arco es el producto del radio por el ángulo central, el ángulo del círculo pequeño debe de ser tres veces más grande que el ángulo del círculo grande. Pero el ángulo del círculo grande debe aumentarse en 2p; por lo tanto el ángulo del círculo pequeño debe aumentarse en 3*2p = 6p, y el círculo pequeño gira (o 'da vueltas', o 'rota') tres veces. La respuesta es incorrecta."

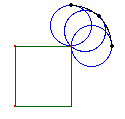Obviamente los expertos trataron de usar la idea Lin. Veamos entonces que resultados se producen usando la idea Cur. Reemplacemos entonces el círculo más grande por un cuadrilátero. Se ve inmediatamente (Figura 6) que en las cuatro esquinas el círculo más pequeño rota sin progresar a lo largo del perímetro de la figura más grande. Al reemplazar el círculo más grande por un cuadrilátero podemos entonces percibir que hay dos rotaciones diferentes superpuestas en el movimiento del círculo más pequeño. Cuando éste gira un ángulo de 90° en cada una de las cuatro esquinas, se entiende inmediatamente que la respuesta correcta debe de ser , cuatro veces!
   Un punto del círculo más pequeño describe una epicicloide que tiene tres "hojas".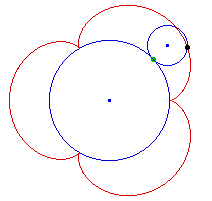 Esto es lo que la idea Lin nos dice. Bob Davis sugiere que los expertos deben haber usado pero aplicado mal esta idea, porque negaron la curvatura o bien las dos rotaciones diferentes del círculo más pequeño.

Para completar la exposición presentamos la solución de Davis:

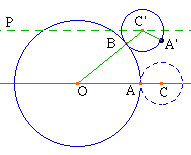
"En la Figura 8, C es el centro del círculo pequeño en la posición de partida. Un momento después de que el movimiento se ha iniciado, el centro se ha desplazado a C'. Dado que no hay deslizamiento, el arco BA' sobre el círculo pequeño tiene la misma longitud de arco que el arco AB sobre el círculo grande. De modo que el ángulo BC'A' es tres veces más grande que el ángulo AOB. Pero, cuando consideramos una línea de referencia que no gira, PC', que se traslada de tal suerte de pasar siempre a través del centro del círculo más pequeño, vemos fácilmente que el ángulo BC'A' NO es el ángulo de rotación del círculo pequeño -- éste ángulo es PC'A. El resto de la solución es ahora cuestión de rutina…. El círculo pequeño gira -- o rota, o da vueltas -- exactamente cuatro veces…. Nótese que la representación incorrecta está cerca de ser correcta. Si una rueda de bicicleta que tiene un perímetro de 87 pulgadas rueda sin deslizarse alrededor de una acera plana, y cubre una distancia de 3*87=261 pulgadas, entonces la rueda habra girado exactamente tres veces. Supuestamente alguna representación cognitiva de este fenómeno ha sido evocada, o construida, por los expertos, de tal manera que todos ellos estuvieron de acuerdo en la respuesta incorrecta" por usar la idea Lin solamente.

Como en el análisis de Papert del problema 1, esta presentación del problema 2 está fuertemente influenciada por la preocupación tradicional por las fórmulas. Las alternativas Leibnizianas, en contraste, se interesan más en la estructura relacional y los objetos intuitivos.

 
(Regreso a la primera pagina)

---

Cabri Java Project