Grenier D. (2000)
Learning proof and modeling. Inventory of Teaching Practice and New Problems.

Contribution to: Paolo Boero, G. Harel, C. Maher, M. Miyazaki (organisers) Proof and Proving in Mathematics Education. ICME9 TSG 12. Tokyo/Makuhari, Japan.

  
II. A new mathematics field for proof and news problems
© Denise Grenier

-> Cover page
-> Part 1

We push to the forefront these three aspects of proof pratice - status of truth, conjectures and modeling - in the learning objectives of our research work. We will detail and illustrate them from suitable typical problems.

II.1. Devolution of problems, stake of truth

One certainly cannot conceive a proof without its relation to a question to be solved, located within a given field of research. In particular, the mathematical situations take a meaning in the course of the various steps :

Problem --> Question --> Hypotheses --> Conjecture --> Reasoning --> Result.

The devolution of a problem is of course directly linked to the meaning it can take. Probably, for a majority of pupils, this meaning is very related to the Didactical Contract. For example, the problem is attached to a concept, to a chapter of the textbook. 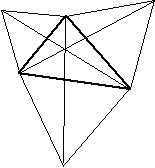The interest of problems which are not already modelled in a mathematical form is that they make it possible to consider this meaning outside a precise mathematical context.
   The explanatory function of proof is a privileged aspect in teaching : a majority of the proofs requested from pupils just relate given results. One interest developped here is the aspect " reduction of doubt " in the proof.
   Geometry in education is primarily what one can call " geometry of incidence " : the interest rests in problems which amount to decide whether points belong to lines or circles, whether lines are concurrent, etc. Thes is no doubt about the result.

We will illustrate our matter by one example.

Let us consider the construction of the " Torricelli Point " : Consider the equilateral triangles constructed on each edge of a given triangle. The goal is to show that the three lines joining a vertex of the triangle to the opposite vertex of the opposite equilateral triangle are concurrent.

The truth of that result can hardly be questioned, especially if the figure is drawn with more accuracy. If a geometry software is used, it can be legitimate to regard the result as undoubtedly true. The proof then cannot be regarded any longer as the best way to establish the truth. However, its role as an explanation remains.
   Of course, it would be feasible to put the question of the Torricelli point, in a more open way. For example, the question could be the following one :

" What is the more economic way to link thre points, like below :

It would be then necessary to study different occurrences, and thus, one can see that the Torricelli point is not always the solution to the question.

II. 2. The specificity of some combinatorial arguments

We present now some methods which play a central role in discrete mathematics, but which, in our opinion, also have a more general range of validity, such as decomposition/recomposition or structuring of objects, in particular by colouring, or the pigeons' holes principle. We will see that a combinatorial point of view makes it possible to develop a new analysis of certain concepts and tools, as induction - which is a fundamental tool for proving.

II. 2.1. Decomposition/recomposition

Decomposition/recomposition is a central method in combinatorics. Paving problems (of which two examples have already been given) are naturally a privileged field of application of this method.
   Let us start by illustrating this through a numerical example which is used as a standard exercise of application of induction : finding the sum of the first N integers. Whereas the induction process by itself does not produce the value of the sum, but simply allows to check that the suggested formula is correct, another reasoning is sometimes invoked, while pointing out its astute, even magic, character.
   Consider the sum to be found as a "staircase", and, assemble two such staircases to form a rectangle.

 

The principle of "decomposition/recomposition" applied to the concept of area (and more generally of volume), which is then seen as a measurement attached to surfaces and defined by its properties of additivity and invariance by recomposition, allows to solve many situations in a simple manner. One can see the example of Euclid's rectangle, in Grenier (1999).

II.2.2. Induction

Induction rests on a particular decomposition : the object is divided in two objects : a smaller object satisfying the same hypotheses, plus another "piece". The basic mathematical object under consideration is the set N of integers. In discrete mathematics, proof by induction is very often constructed according to the following scheme :

- argue by contradiction : there exists a counterexample (of size n) ;

- find a minimal counterexample (of size n0) ; the following property is used : every nonempty subset of N has a smaller element ;

- consider a " smaller object " so as to reach a contradiction (this smaller object is rather frequently obtained by " breaking " the initial object : removing vertices in a graph, partitioning a polymino...).

This scheme of proof may allow to obtain an inductive construction of a class of objects starting from more basic terms. On the other hand, to be able to use the " ascending " scheme of the type :

P(n0)
and for every n „ n0, P(n)->P(n+1),

it is necessary to know how can constructed all the (n+1) objects from a n-object..
   It is true that in the overwhelming majority of school exercises, one builds only N (and not a class of objects ordered by N). : P(n) is an analytic expression f(n) and f(n+1) can be easily written.
   We are aware that the combinatorial point of view about induction rests on the contradiction principle. However, in the teaching activity, this type of reasoning seems to be carefully avoided. Would it be because the contradiction principle is considered to present serious difficulties to pupils ? In fact, is it really possible to make mathematics without having an equal freedom to consider claims which would be true or false ?
   Let us illustrate this combinatorial point of view on induction. We let the reader appreciate, in what follows, the similarities and differences with the " usual " reasoning by induction : in particular, it can be noticed that the induction involved is not well founded and that the property settled does not depend on the induction parameter.
   The question is the following one :

" For what values of n, does it exist a regular n-polygon with integer coordinate vertices (of which one can put the n vertices on the squared grid) ? "

     examples with n=4 and n=8

The proof consists in establishing the following result :

" In the plane, there are no regular polygons with integral coordinate vertices, except squares. "

 

For this, notice first of all the equivalence between the existence of equilateral triangles with integral coordinate vertices and the existence of regular hexagons with integral coordinate vertices.
   We will thus show that there are no regular polygons with integral coordinate vertices possessing more than 4 vertices.

Proof :

Suppose that x1, x2, x3... are vertices of the polygon P, oriented according to positive trigonometrical orientation. With each vertex xi, take the point x'i obtained from vertex xi+1 by a rotation of ¼ /2 around xi. One thus obtains a polygon P' whose nodes are x'1, x'2, x'3...
   If P is regular, so is P', and in this case, if P has more than 4 vertices, the vertices of P' are located inside P. If P has integral coordinate vertices, so has P'.
   With any polygon drawn in the plane, one can associate the number of points with integral coordinates located inside this polygon ; this number will measure its " size ".

Let us consider a minimal counterexample, in other words, a regular polygon P (with more than four vertices), of the smallest possible size, whose vertices have integral coordinates. Let P' be the polygon obtained from P by the above construction. P' is a regular polygon with more than four vertices, with integral coordinate vertices, of size strictly smaller than that of P. Contradiction.

II.3. A " fundamental " situation

We suggest here a situation which gives a possibility, in a spontaneous or guided way, that some of the main combinatorial methods emerge. We make the assumption that this situation can be regarded as a fundamental situation (in the meaning of Brousseau).
   The question is the following one :

" Is it possible to tile, with dominos, a given " odd " polymino with a deleted square ? ".

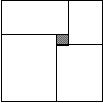
If it is possible to find a tiling, the question is solved, but only for the given particular occurrence. However, in general cases, after several unsuccessful attempts, a proof is needed.
   Let us examine the particular problem of paving of a square polymino by dominos, as presented here in a particular case (n=7, and a given position of the deleted square) :

 

The problem suggested to pupils is whether there exists a paving of a square polymino with an elementary square removed. This situation has been tested at various levels : collège (2nde, 1ère, Terminale), DEUG, teachers during their trainingcurriculum, teachers in activity. The strategies used for solving, the difficulties encountered during various experiments are rather similar. The initial steps adopted to attack the problem are not very distant from those of the professional researcher : experimentation on simple cases, formulation of conjectures and, more rarely, attempts of modeling and structuring. Let us give some more details.

a) Tests on small cases (squares of side 2, 3, 4...).

While this is not necessarily regarded as a "result", it appears very quickly that a polymino can be paved only when the number of elementary squares is even. One thus considers only the squares of odd side in which an elementary square has been removed. After some tests, it is realized that certain squares do "work": if an elementary square is removed, the remaining part can be paved. These squares are shown in black on the figure.

 

This leads to the conjecture :

" when the removed square belongs to the set of black boxes ("good" boxes), it is possible to pave by dominos. Otherwise, it seems that paving is not possible. "

b) Modeling and structuring

The problem is to pave by dominos; however, what is a domino? Two adjacent squares.
   It is thus the relation of vicinity between squares which is significant. One can notice that to two different polyminos different can also correspond a relation of vicinity.

 

This relation of vicinity can be modelled by the graph :

 

These two polyminos are equivalent with respect to the problem of paving by dominos.
   One can thus become aware that the activity of modeling can consist in getting rid of superfluous information.
   How can this relation of vicinity on the polymino become apparent ? Is it possible to locate a square with respect its neighbours ? One thus arrives to the idea of structuring the polymino by colours : the squares are colored so that two adjacent elementary squares do not have the same color. This is carried out by colouring squares in black and white as in a chessboard. One can then formalize more precisely the distinction between " good " and " bad " squares conjectured at the beginning.
   The use of a colouring scheme makes it possible to obtain a proof of the impossibility of paving when a "bad" square (i.e. a square of the less numerous color) is removed. Indeed, a domino always covers a white square and a black square, so that a polymino can be pavable only when there are as many black squares than white squares when a chessboard colouring scheme is used.

c) Necessary / Sufficient conditions and Decompositions

One can thus considerate the question of the diffrence between necessary condition (NC) and sufficient condition (SC). A first necessary condition had appeared from the very beginning : the parity of the number of squares. But this condition was too simple to be regarded as a true NC. In any case, it did not have any chance to be perceived as a good candidate to be a NSC (necessary and sufficient condition).

Counterexamples are in fact quickly found, the one with smallest size being :

The second NC - equality of the number of black squares and the number of white squares - seems more serious. Amongst other things, it gives a proof which is different from the examination of all the cases, of the non-pavability of found counterexamples. Is it sufficient ? Non connected counterexamples are hardly convincing :

 

However, separate pieces can be joined to obtain "balanced" connected polyminos which are not pavable.

 

One will see, by decomposition, that this condition is also sufficient for solving the case of a square polyminos in which an elementary square is removed.

• Break up the square into smaller pavable parts (for example in rectangles having an even side). Several partitions can appear, the simplest being the following :

In this partition, the rectangles have their two sides of different parity. This decomposition gives an algorithm for paving, therefore a validation of the proof. The search for partitions reveals difficulties related to confusions between NC/SC. In the case when paving is impossible, the production of partitions which "do not work" is frequently given as a proof of impossibility; quite often, one sees a formulation of the conjecture :

"pavable" U "non pavable" = "non pavable".

 

• Other partitions leading to smaller squares are also proposed

In this way, one is no longer very far from a reasoning by induction
   The first partition has been produced by pupils of 2ème and 1ère classes.
   The second was proposed in DEUG and by students of IUFM : the odd square in which one ("good") elementary square is removed has been partitioned in a L-shaped tape, pavable, and a smaller square with odd side, in which again a (" good ") elementary square is removed. This type of partition is always possible, except for an initial square of side 1 and for a square of side 3 with the central elementary square removed. These two cases will be the bases of the induction.
   One can be tempted to carry out a simpler partition, for example to divide in two parts by an horizontal or vertical line : the square is then divided in two rectangles. If one then considers the more general class of odd side rectangles with an elementary square removed, the proof continues to work ... A more general result is thus obtained. One can illustrate in this manner the fact that by modifying adequately an induction hypothesis, easier proofs can often be obtained.

• The relation of adjacency between squares - the graph model - and the structuring by colours eventually lead to a third type of proof for sufficient condition.
   The odd square is covered by a " path ".

If a black square is removed, the path is shared in two even paths which are both pavable. This idea of using a path is approached by some pupils, probably suggested by observation of neighbouring dominos.

Return to cover page

Go to part 1