Proof and perception III (Suite) by Michael Otte Institut für Didaktik der Mathematik Bielefeld, Germany   Problem 1 Our first problem is taken from S. Papert's book "Mindstorms" (Basic Books 1980, 146): 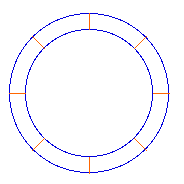"Imagine a string around the circumference of the earth, which for this purpose we shall consider to be a perfectly smooth sphere, four thousand miles in radius. Someone make a proposal to place the string on six-foot-high poles.    Obviously this implies that the string will have to be longer. A discussion arises about how much longer it would have to be.    Most people who have been through high school know how to calculate the answer. But before doing so or reading on try to guess: Is it about one thousand miles longer, about a hundred, or about ten?" Papert then suggest looking first for a similar but simpler version: 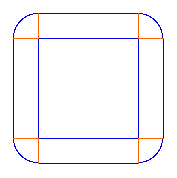 "A good general rule for simplification is to look for a linear version. Thus we pose the same problem on the assumption of a 'square earth'". Increasing the size of the square does not change the quarter-circle slices, such that the extra string needed to raise a string from the ground to height h is the same for a very small square earth as for a very large one. This solves the problem.    The amount of extra string needed is (2ph). Papert himself says that the purpose in working on the problem is not "to get the right answer", but to "look sensitively for conflict between different ways of thinking about the problem" (ibid.).     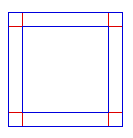A different way and perhaps, more consistently, Leibniz might suggest as a linear version:       But Papert wants to continue, thus: Nevertheless, both may point to the fact that their idea shows that the size of the "earth" makes no difference to how much extra string is needed. That eventually solves the problem. Thus both ideas, let us call them Cur, (the idea of curvature) and Lin (the idea of linearity) respectively appear equivalent with respect to the problem at hand. Drag the green point    But both ideas yield more. 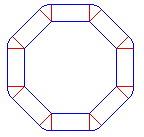Lets start with the Leibniz version and lets for every polygon (square, octagon...) call the shortest distance from the center to the perimeter the radius of that regular polygon. Increasing the radius by h increases the length of the perimeter by "the perimeter of a similar polygon of radius h". This is exactly the linearity of the function represented by the geometric form itself. The whole is the sum of its parts: If the radius grows from x to (x+h) the perimeter increases from f(x) to f(x)+f(h).    Therefore we have f(x+h) = f(x) + f(h) and f(o) = o. The perimeter of a polygon is a linear function of its radius. And the principle of continuity yields the same result for the circle (remember that Leibniz was the first to systematically employ this principle). The important thing is that you can read this fact directly off from the geometric figures. You can see with your own eyes that the enlargement of the perimeter is represented again by a polygon of the same shape. To derive another, more constructive than descriptive representation of the linear function, Leibniz would point to the fact that the shape of the polygon is not changed by putting the string around on poles (i.e. enlarging the radius by h). 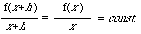et y = f(x) = c.x Both ways give an illustration of the idea of a formbased conceptualization. The potentialities of the Papert's idea Cur can only be appreciated as soon as one considers the algebraic expression y = c.x as the new and relevant shape. Different from Leibniz we then get one and the same linear function y = 2p.x for all types of "earth's" (in fact the perimeter may be any smooth closed curve without self-intersection). The proportionality factor 1.(2p) gives the number of full circles which the heads of the poles run through when following the curve. Therefore alternative values of c would be (n.(2p) (n being any integer) and from the discreteness of the range we understand immediately that small deformations of the curve cannot change the value of c. The geometric object in question is no longer the curve, but a vector field along a curve. The integer n is usually called the index of that vector field with respect to the curve. The index will not change as long as deformations of the curve do not pass through a zero of the vector field.    We might derive from this an easily understandable argument justifying Brouwer's Fixed-Point Theorem. Both approaches solve problem 1 and from this point of view appear as equivalent. We shall now present a second problem with respect to which the ideas Cur and Lin will prove inequivalent. We take this problem (a problem about the epicycloid) from Robert Davis' book "Learning Mathematics" (Croom Helm, London 1984, 216pp.). Problem 2 "In a recent ETS test, one question dealt with a small circle that rolls, without slipping, around the outside of a larger circle. (Thinking of them, if you wish, as gears.) The radius of the large circle is three times the size of the radius of the small circle. ... How many times do we see the small circle revolve ..." Drag the green point Bob Davis continues: "The experts apparently reasoned essentially as follows: if the radius of the larger circle is three times as great, then the perimeter is three times as great. 'Rolling without slipping' means that the arc-lengths are equal. Since the arc-length s is the product of radius times central angle, the angle for the little circle must be three times as great as the angle for the larger circle. But the angle on the large circle must increase by 2p; therefore, the angle for the small circle must increase by 3.2p = 6p, and the small circle revolves (or 'turns', or 'rotates') three times. This answer is wrong". 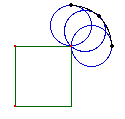Obviously the experts tried to use idea Lin. Let us therefore see which results idea Cur will produce We thus again replace the larger circle by a quadrangle. We see immediately (fig. 6) that at the four corners the smaller circle rotates without making progress along the circumference of the larger figure. By replacing the larger circle by the quadrangle we become able to perceive that two different rotations are superimposed in the motion of the smaller circle. The quadrangle separates, so to speak, these two movements of the smaller circle. As it rotates by an angle of 90° at each of the 4 corners, we immediately understand that the correct answer must be, four times!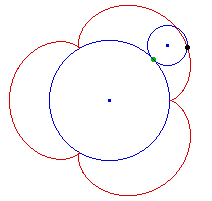    A point of the smaller circle describes an epicycloid which has 3 "leaves" (fig. 7). This is what idea Lin tells us. That the experts must have used this idea and misapplied it because they neglected the curvature or rather the two different rotations of the smaller circle is also suggested by Bob Davis. For the sake of completeness we present Davis' solution: "In [the following figure], C is the center of the small circle in the starting position. A moment after the motion starts, the center has moved to C'. Because of non-slipping, arc BA' on the small circle has the same arc-length as arc AB on the large circle. Therefore angle BC'A' is three times the size of angle AOB. But, the moment we have available to us a non-rotating reference line, PC', that translates so as always to pass through the center of the smaller circle, 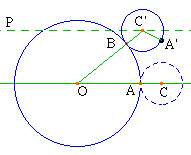we see easily that angle BC'A' is NOT the angle through which the small circle has rotated. Instead, angle PC'A' is. The rest of the solution in now routine ... The small circle revolves -- or rotates, or turns -- exactly four times. ... Notice that the wrong representation comes close to being right. If a bicycle wheel that has a perimeter of 87 inches rolls without slipping along a flat sidewalk, and covers a distance of 3.87 = 261 inches, then the wheel will have rotated exactly three times. Presumably some cognitive representation of this phenomenon was retrieved, or constructed, by the experts, so that they all agreed - on the wrong answer" because of using idea Lin only. Like Papert's analysis of problem 1, this presentation of problem 2 is very strongly influenced by the traditional concern for formulas. The Leibnizian alternatives, in contrast, are more interested in relational structure and intuitive objects.   (Back to the first page) Cabri Java Project