De la preuve, de la logique de la pratique
de l'enseignement de la géométrie et
du standard US de la "preuve sur deux colonnes "

Dans l'enseignement des mathématiques, aux Etats-Unis d'Amérique, la démonstration est habituellement associée à un cours annuel de géométrie, au lycée (high school) et à une forme spécifique : la preuve sur deux colonnes. Sekiguchi (1991), dans une étude ethnographique de l'un de ces cours de géométrie, décrit ce format de la façon suivante :

On trace un long trait horizontal et une trait vertical partant en son milieu pour former un T, créant ainsi deux colonnes sous le trait horizontal. Dans la colonne de gauche on écrit une séquence déductive d'énoncés conduisant à la conclusion recherchée, en numérotant chacun des énoncés. Pour chaque pas de déduction, on doit écrire dans la colonne de droite la justification avec le nombre correspondant (pp. 78-79).

Les raisons données pour chaque énoncé précisent en générale une hypothèse (une donnée), un postulat, un théorème ou une définition (une et un seule par ligne) sur laquelle ou lequel l'énoncé est appuyé.

Une preuve sur deux colonnes (tiré de Clemens et al., 1994, p. 301).
Figure 1

Les preuves sur deux colonnes et la logique de la pratique

L'observateur d'une leçon au cours de laquelle est produite une preuve sur deux colonnes aura probablement le sentiment qu'il y a plus à dire à propos de ce format que ce qui suggéré par une simple mention de sa mise en page particulière. En fait, cet observateur remarquera peut être que, au-delà de la différence de format entre la preuve sur deux colonnes et les démonstrations de géométrie d'un texte mathématique (e.g., in Hilbert, 1899/1971), il y a aussi d'importantes différences qui touchent au fond (ce qui peut être dit, ce qui peut être omis, ce qui doit être dit et comment, etc.). Aussi, bien que pour introduire ma discussion j'ai relevé dans la preuve sur deux colonnes le format (comme une sorte de bouc émissaire), cette discussion vise le processus de construction réciproque de la forme et du contenu qui s'établit dans la logique de la pratique de l'enseignement de la géométrie. Vygotsky a attiré notre attention sur le rôle central des outils et des signes dans la construction de l'action humaine, comme Wertsch (1991) le cite :

"By being included in the process of behavior, the psychological tool alters the entire flow and structure of mental functions. It does this by determining the structure of a new instrumental act, just as a technical tool alters the process of a natural adaptation by determining the form of labor operations." (pp. 32-33)

Si le format de la preuve sur deux colonnes est comme tel un outil technique dans l'enseignement de la géométrie aux Etats-Unis, il semble raisonnable de poser la question de savoir comment sa présence dans la pratique façonne (et est façonnée par) le savoir enjeu d'enseignement.
   Comme pour la présentation de toute démonstration, les pratiques initiales et le rôle des agents engagés dans la production d'une preuve sur deux colonnes sont occultés au profit des pratiques textuelles réglées par une économie particulière de la communication. Dans ce cas, l'organisation des éléments de cette pratique textuelle offre à un lecteur bien particulier la fiction d'une reconstruction de la production d'une preuve. Ce qui est montré peut être à peu près lu comme un catéchisme -- une séquence uniforme de phrase du type "(je dis ceci) parce que (cette raison)". L'argument mathématique suit ou non, mais il peut certainement "être suivi", dans la mesure où les raisons imposent une métrique uniforme qui détermine ce qui constitue une liste acceptable (complète) d'énoncés : la conséquence d'un énoncé donné doit toujours se trouver à distance d'une "raison". Le résultat en est que la preuve peut être examinée en suivant une check list -- chaque ligne de la preuve -- et vérifiée par l'adéquation de l'appariement des énoncés et des raisons -- indépendamment de leur pertinence stratégique pour l'ensemble de la construction. Il s'en suit qu'une preuve peut parfois être rejetée après un pas particulier, au motif que "les choses s'engagent mal", en revanche cela permet aussi que tout ce qui a été fait avant ce pas soit conservé puisque marqué "OK" jusque là.
   Tout ceci peut être le cas des formes habituelles d'écriture mathématique ; le format de la preuve sur deux colonnes est une forme institutionnelle de coercition pour s'assurer que ces choses là ont lieu effectivement. La preuve sur deux colonnes fonctionne comme fonctionne l'injonction implicite de "montrer son travail" dans le cas de la division (à l'école élémentaire aux Etats-Unis, voir la figure 2). Pour que son travail soit reconnu dans le cas de la division, l'élève doit écrire tous les produits partiels (comme 56 ou 84) et faire explicitement les soustractions : en particulier ces étapes montrent l'origine de dividendes intermédiaires comme 98 ou 144, et de cette façon légitime leur présence. Dans la pratique de la division, la présence de tous les pas du calcul sur le papier ne va pas seulement de concert avec la maîtrise de la procédure par l'élève, mais aussi avec l'efficacité du contrôle de l'enseignant sur l'apprentissage (de la procédure) par l'élève et avec l'identification de la connaissance en jeu (connaître la division signifie savoir mettre en oeuvre la procédure).

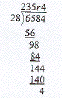
Une division. Figure 2.

Comme l'algorithme de la division est adapté à l'objectif de trouver un quotient et un reste, le format de la preuve sur deux colonnes est adapté à la tâche de proposer une démonstration. Mais ce genre de preuve n'est pas réellement destiné à être présenté à une communauté qui aurait à établir la validité d'une proposition (Balacheff 1987 p.147). La preuve sur deux colonnes est plutôt, comme la division avec ses produits partiels et ses divisions, proposée à un enseignant dont le projet n'est pas d'être convaincu de la validité d'un énoncé ou éclairé par l'idée d'une preuve. Le projet de l'enseignant n'est pas non plus de se réjouir de l'élégance d'un argument, il est de verifier, pour chaque exercice de preuve, jusqu'à quel point la séquence de pas qu'il examine est complète.    La preuve sur deux colonnes n'a pas dans la classe le rôle de la démonstration dans la communauté mathématique. Au contraire, une preuve sur deux colonnes est un exercice de routine dont le but est de pouvoir être reproductible (i.e. les enseignants produisent des preuves pour donner un modèle de ce que les élèves doivent faire, et les élèves produisent des preuves pour apprendre comme les faire).

L'apprentissage de la démonstration, en s'appuyant sur l'utilisation de la preuve sur deux colonnes, peut être perfectionné par petites touches (chercher des énoncés "intermédiaires", chercher la "bonne" raison). Cependant le transfert de la connaissance acquise pour l'une de ces preuves à d'autres situations qui la solliciterait, peut être complètement différent de savoir "comment produire" la preuve -- de la même façon que la connaissance de l'algorithme de la division ne semble pas garantir la compréhension par l'élève de la signification de la division (voir Schoenfeld 1998, en particulier le problème des bus p.150, et le problème de construction d'une preuve pp.152-158).

En cette époque favorable, où l'importance de la preuve revient dans la réthorique Nord Américaine sur l'enseignement des mathématiques (see Kilpatrick, 1997; Wu, 1997; Ross, 1998; NCTM, 1998, pp. 80-85), le moment semble venu de discuter des nuances autour des notions de preuve, de démonstration, de preuve sur deux colonnes, d'argumentation, etc. Mon propos n'est pas seulement d'indiquer qu'il y a plus à faire pour la démonstration que l'utilisation du format de la preuve sur deux colonnes. Cette considération relèverait du lieu commun et les standards du NCTM (1989) ont bien mis en première place en recommandant d'augmenter l'attention aux "arguments déductifs exprimés oralement ou par mises en formes en phrases ou paragraphes" (p.126) et porter moins d'attention aux "preuves sur deux colonnes" (p.127). Au contraire, mon propos est de dessiner les grandes lignes du rôle joué dans la pratique de l'enseignement de la géométrie par des formats tels celui de la preuve sur deux colonnes dans le façonnage de conceptions de la géométrie, du raisonnement et de la démonstration. Une telle entreprise peut apporter des éléments pour la critique d'une croyance de caractère idéologique, et par là contestable, de ce que l'utilisation du format de la preuve sur deux colonnes dans la classe aurait à voir avec l'idée de fournir aux élèves une expérience de la rigueur et du formalisme en mathématique.
   D'une part, les impératifs culturels selon lesquels l'enseignement des mathématiques devraient viser à reproduire les conditions de la production des savoirs mathématiques impliquent que les mathématiques scolaires donnent la possibilité aux élèves d'apprendre à démontrer, leur permettent de fréquenter des preuves culturellement pertinentes, et les familiarisent avec la signification de la démonstration dans la construction et la validation des savoirs mathématiques. D'autre part, un apprentissage signifiant des mathématiques sera probablement favorisé par des pratiques qui ressembleraient à celles de la production des savoirs mathématiques. Dans la mesure ou rigueur et formalisme servent les mathématiciens non seulement pour la validation mais aussi pour la construction des savoirs, rigueur et formalisme sont des ingédients naturels des pratiques dans lesquelles les connaissances mathématiques peuvent être construites de façon signifiante. Comme l'énonce le Draft for the Standards 2000 :

It should be stressed that exploring, conjecturing, representing, and proving are all deeply connected aspects of mathematical thinking. "Reasoning" and "Proof" should not be thought of as separable from the bulk of mathematical activity. (NCTM, 1998, p. 85)

Vu les simplifications habituellement exagérées de la réthorique éducative, il semble important de noter qu'une insistance accrue sur l'argumentation et la démonstration est bien sûr consistante avec l'objectif de donner aux élèves des occasions de s'engager dans des pratiques mathématiques (de même que rigueur et formalisme dans la pratique mathématique sont productives plutôt que restrictives). Mais cette plus grande insistance n'implique pas que soit enseignée explicitement la preuve sur deux colonnes (ou tout autre format), ni ne donne de garanties que la pratique de la preuve sur deux colonnes assurera une expérience de la rigueur ou du formalisme mathématique.
   Un premier essai, de portée plus large, sur les relations particulières entre démonstration, formalisme et argumentation, est présenté dans une version plus longue du présent texte (Herbst, 1999) dans laquelle sont discutées quelques conjectures sur les circonstances historiques qui ont donné naissance aux pratiques de la preuve sur deux colonnes dans l'histoire de l'enseignement des mathématiques aux Etats-Unis. La place de la preuve sur deux colonnes dans la pratique de l'enseignement et dans l'apprentissage des mathématiques s'est constituée en interaction avec quelques objets de discours tels que démonstration, géométrie et raisonnement. Les caractéristiques de ces interactions rendent partiellement compte de la resistance du format de la preuve sur deux colonnes et de son association possible à la rigueur et au formalisme.
   Les premiers chapitres d'une histoire de la preuve dans les enseignements secondaires (high school) des mathématiques aux Etats-Unis prennent place dans l'étude de la géométrie. La version plus longue du présent texte analyse les modifications de la notion (ou ce qui en tient lieu) d'étude de la géométrie comme témoignage des conceptions changeantes de la démonstration, du raisonnement et de la géométrie elle-même. Les raisons de la robustesse de la preuve sur deux colonnes doivent être recherchées non dans les circonstances ponctuelles de son origine (telles que "quand a-t-elle été inventée ?" ou "par qui ?") mais dans les caractéristiques intrinsèques des pratiques qu'elle a servies et des pratiques que sa présence a rendu possibles. Ce qui suit a touvé un soutien dans la recherche historique présentée dans la version plus longue de ce texte.

Quelques commentaires sur le format de la preuve sur deux colonnes

En m'appuyant sur l'observation des pratiques actuelles de l'écriture de démonstrations dans l'enseignement secondaire, j'ai conclu (Herbst, 1998, pp. 239, 271) que la preuve sur deux colonnes fonctionne de façon solidaire avec une division du travail discursif de l'enseignant et de l'élève. Ce format assure l'enseignant d'un critère implicite pour indiquer ce qui doit être dit (et donc laisse sans question le contrôle sur les opérateurs épistémiques tels que connaître, nécessaire, pouvoir dire, etc.). Ce format rend l'élève responsable de la production d'une liste ordonnée d'énoncés "catégoriques" à propos d'une figure donnée, alors qu'il réserve à l'enseignant la décision de considérer que la liste produite constitue un argument valide.
   Ces observations peuvent expliquer pourquoi la preuve sur deux colonnes est peut être mieux adaptée à la logique ou à la pratique de l'enseignement de la géométrie que d'autres formes (moins réglées) d'argumentation. Du point de vue de l'enseignant, ce format constitue un outil efficace pour assurer et contrôler la production d'une preuve acceptable par l'élève. Du point de vue de l'élève, ce format ne le rend par responsable de la construction ou de l'explication de la géométrie enjeu de connaissance ou de la conception d'un argument. Au lieu de cela, il ne requiert de l'élève que la production d'observations empiriques sur la figure considérée.
   La preuve sur deux colonnes définit aussi les limites de ce qui peut être donné à démontrer au sens où elle façonne les conceptions de ce que peut être la géométrie. Elle fonctionne mieux avec une conception de la géométrie comme étude des figures qui ont déjà été effectivement construites ou qui sont constructibles. L'étude de la géométrie selon cette conception est une étude descriptive gouvernée par une logique générale qui insiste sur les connections logiques entre des propriétés factuelles. Pour être clair, la géométrie euclidienne est bien sûr tout cela, mais nécessairement n'est pas réduite à cela. Les pratiques mise en évidence autour du format de la preuve sur deux colonnes semblent décourager une conception complémentaire de la géométrie qui était centrale dans les Eléments d'Euclide et dans les notions mises en oeuvre dans la géométrie grecque (Caveing 1990) : la géométrie est aussi l'étude des conditions qui font que les figures sont constructibles. Dans l'étude de la géométrie dans cette dernière conception, les liens logiques entre les énoncés sont pondérés par la force substantielle de ces liens ; ce qui rend une proposition intéressante n'est pas seulement qu'une preuve existe mais aussi que sans une preuve on ne peut pas réellement savoir si cette proposition est valide ou non (de par le saut qu'il peut y avoir entre les hypothèses et la conclusion). Parce que la pratique de la preuve sur deux colonnes a besoin de la donnée d'une figure, des énoncés des hypothèses et de ce qui est à démontrer, la conception de la géométrie comme étude des conditions nécessaires et suffisantes est désinvestie (et on peut comprendre pourquoi les élèves peuvent approcher par essais et erreurs un problème de construction après avoir établi un énoncé qui entraîne la procédure de construction -- voir Schoenfeld 1988).

Le format de la preuve sur deux colonnes contraint les conceptions possibles de la démonstration et de l'activité de preuve en mathématiques. En séparant l'origine des énoncés qui sont formulés des arguments qui sont énoncés à leur propos, ce format renforce le rôle de la preuve comme méthode de certification, séparée de la recherche de la connaissance ou de la construction des objets mathématiques enjeux de connaissance. En évinçant l'énoncé de la preuve et permettant de maintenir l'ordre dans les énoncés qui constituent la preuve, le format de la preuve sur deux colonnes rompt la dialectique entre formulation et validation décrite par Lakatos (1976 ; voir aussi Balacheff 1991) et la tension sous-jacente entre l'intérêt d'une connaissance et sa validité.
   De ces observations, on peut aussi tirer que les pratiques associées au format de la preuve sur deux colonnes court-circuitent les caractéristiques épistémologiques du raisonnement mathématique. Ces pratiques entretiennent une réduction du raisonnement mathématique à une activité mettant en jeu la psychologie d'agents raisonnant et la langue "naturelle" qu'ils associent à un monde mathématique "donné". Le raisonnement mathématique devient tout simplement un raisonnement logique (général) appliqué à des objets mathématiques dont les conditions d'existence sont considérées comme données. Bien sûr le raisonnement mathématique engage le raisonnement logique, mais ce qui est problématique est l'exclusion des aspects épistémologiques spécifiques des objets mathématiques sur lesquels et avec lesquels on raisonne. En identifiant la précédence logique des "raisons" à leur précédence temporelle dans le texte, le raisonnement mathématique devient plus encore une activité de description d'un monde mathématique "donné" plutôt que celle de construction d'un monde mathématique "possible" (ou mathématisation). Quelques conséquences concernant la valeur des mathématiques pour l'éducation générale et concernant la nature des transferts (de l'étude des mathématiques à d'autres situations) peuvent être envisagées (voir Judd 1928 ; Skovsmose 1992 ; Vygotsky 1934/1986 pp. 146-209) : le raisonnement mathématique devient un moyen adapté pour raisonner sur des objets purement mathématiques ou qui ont été déjà mathématisés ailleurs (comme ceux des sciences dures), mais est à peine apte à permettre un raisonnement sur d'autres objets (comme ceux des sciences molles et de la vie quotidienne) au-delà du niveau des apparences. En entretenant l'idée de la notion de preuve comme seulement un raisonnement logique sur des objets qui sont déjà mathématiques, le format de la preuve sur deux colonnes contribue à arrêter la dialectique scientifique entre empiriscisme et rationalisme dans la construction des objets mathématiques du discours (voir Skovsmose, 1992, p. 6).

Une conclusion provisoire

Une version plus longue de ce texte (Herbst, 1999) propose quelques conjectures sur les circonstances historiques qui ont permis l'avènement du format de la preuve sur deux colonnes et sa robustesse pendant la première moitié du siècle aux Etats-Unis. Le format de la preuve sur deux colonnes lui-même n'est pas resté inchangé, mais s'est adapté pour satisfaire l'évolution des caractéristiques de la logique de la pratique qu'il sert. Considérant la plausibilité de ces conjectures historiques, j'ai défendu que l'interaction entre le format de la preuve sur deux colonnes (aux formes changeantes) et (les conditions changeantes de) l'étude de la géométrie a contribué de façon significative à façonner une conception de la géométrie (scolaire) comme étude descriptive des figures géométriques, une conception de la démonstration comme une simple méthode de certification de la connaissance et une conception du raisonnement mathématique réduit à un raisonnement logique sur des objets de connaissance mathématique "donnés".
   Ces effets plausibles, et pas seulement la forme matérielle de la preuve sur deux colonnes, sont ce qui nous intéresse ; comme on le notera peut être, les ouvrages scolaires actuels incitent parfois l'élève à écrire des preuves dans un autre format (texte organisé en paragraphes ou d'organigrammes, voir Rubinstein et al., 1995, p. 396) mais ce qui a été dit du format de la preuve sur deux colonnes pourrait être dit tout aussi bien de l'enseignement explicite d'autres formats possibles.
   Du point de vue du lecteur, le produit fini ressemble à un disours qui valide la proposition énoncée. En regardant de plus près on constate que ce produit peut ne pas avoir plus de signification que les protocoles utilisés par les notaires ou les avocats, de même à vrai dire que la division du travail dans la pratique qui produit cette preuve ne ressemble pas à la division du travail dans une communauté de mathématiciens élaborant une preuve en mathématique. Les preuves sur deux colonnes peuvent être qualifiées de formelles, mais leur formalisme a peu de choses à voir avec la rigueur et le formalisme féconds qui aident les mathématiciens à avancer la connaissance humaine des mathématiques (Thurston, 1995). Ces formats jouent un rôle important dans la logique de la pratique de l'enseignement de la géométrie, mais ils n'entraînent pas nécessairement les élèves dans une expérience de la rigueur et du formalisme mathématique.

Références

Balacheff, N. (1987). Processus de preuve et situations de validation [Processes of proof and situations of validation]. Educational Studies in Mathematics 18, 147-176.

Balacheff, N. (1991). Construction et analyse d'une situation didactique: Le cas de "la somme des angles d'un triangle" [Construction and analysis of a didactic situation: The case of "the sum of the angles of a triangle"]. Journal fur Matematikkdidaktikk 12, 199-264.

Caveing, M. (1990). Platon, Aristote et les hypotheses des mathematiciens [Plato, Aristotle, and the hypotheses of mathematicians]. In J.-F. Mattei (Ed.) La naissance de la raison en Grèce: Actes du congres de Nice Mai 1987 (pp. 119-128). Paris: Presses Universitaires de France.

Clemens, S., O'Daffer, P., Cooney, T., & Dossey, J. (1994). Geometry. Menlo Park, CA: Addison-Wesley.

Herbst, P. (1998). What works as proof in the mathematics class. Unpublished doctoral dissertation, The University of Georgia, Athens.

Herbst, P. (1999). On proof, the logic of practice of geometry teaching and the two-column proof format: Some historical considerations. On-line article.

Heilbron, J. L. (1998). Geometry civilized: History, culture, and technique. Oxford: Clarendon Press.

Hilbert, D. (1971). Foundations of geometry. (L. Unger, Trans., P. Bernays, Rev.). La Salle, IL: Open Court. (Original work published in 1899)

Judd, C. H. (1928). The fallacy of treating school subjects as "tool subjects." In J. Clarke & W. Reeve (Eds.), The National Council of Teachers of Mathematics Third Yearbook: Selected topics in the teaching of mathematics (pp. 1-10). New York: Bureau of publications of Teachers College, Columbia University.

Kilpatrick, J. (1997). Confronting reform. The American Mathematical Monthly, 104, 955-962

Lakatos, I. (1976). Proofs and refutations: The logic of mathematical discovery (J. Worrall & E. Zahar, Eds.). Cambridge: Cambridge University Press. [Trad. Française: Paris, Editions Hermann 1985]

National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: NCTM.

National Council of Teachers of Mathematics. (1998). Principles and standards for School Mathematics: Discussion Draft Standards 2000. On-line at www.nctm.org.

Ross, K. (1998). Doing and proving: The place of algorithms and proofs in school mathematics. American Mathematical Monthly 105, 252-255.

Rubinstein, R., Craine, T., & Butts, T. (1995). Integrated mathematics 2. Evanston, IL: McDougal Littell.

Schoenfeld, A. (1988). When good teaching leads to bad results: The disasters of "well-taught" mathematics courses. Educational Psychologist 23(2), 145-166.

Sekiguchi, Y. (1991). An investigation on proofs and refutations in the mathematics classroom. Unpublished doctoral dissertation, The University of Georgia, Athens.

Skovsmose, O. (1992). Democratic competence and reflective knowing in mathematics. For the Learning of Mathematics 12(2), 2-11.

Thurston, W. (1995). On proof and progress in mathematics. For the Learning of Mathematics 15(1), 29-37.

Usiskin, Z., Hirschhorn, D., Coxford, A., Highstone, V., Lewellen, H., Oppong, N., DiBianca, R., and Maeir, M. (1997). The University of Chicago School Mathematics Project: Geometry. (2nd ed.). Glenview, IL: Scott Foresman.

Vygotsky, L. (1986). Thought and language (Alex Kozulin, Trans. & Ed.). Cambridge, MA: MIT Press. (Original work published in 1934)

Wertsch, J. V. (1991). Voices of the mind: A sociocultural approach to mediated action. Cambridge, MA: Harvard University Press.

Wu, H. S. (1997). The mathematics education reform: Why you should be concerned and what you can do. The American Mathematical Monthly 104, 946-954.

Retour à la Lettre