The Strengthening of Proof
in Elementary Geometry
at the turn of the 20th Century
by
Michel Guillerault
Laboratoire Leibniz
Grenoble - France
Near the end of the 19th century and at the beginning of
the 20th century, starting with M. Pasch and especially
following D. Hilbert (Grundlagen der Geometrie
,1899), an attempt was made to establish elementary geometry
on a solid basis, no longer implicitly referring to the
details of certain particular figures.
Here we present the contribution to this
debate of a relatively modest professor of preparatory
classes for the French "Grandes Écoles ",
apparently largely forgotten in our time: Louis
Gérard, professor at Lyon and then at Paris,
specialist in non-Euclidean geometry (Thesis, 1892) and very
careful to present the theorems of elementary geometry in
the most rigorous possible manner. Editor of the Bulletin
de Sciences mathématiques et physiques , he
published in it numerous notes on this subject, and is the
author (with one exception) of each of the passages cited
below. In particular, he was the indefatigable promoter of
the orientation of the angle between two lines, a notion
which permits us to give numerous geometrical propositions
absolute generality, independent of the details of the
illustrating figure.
Over the centuries, the work of Euclid has served, with
greater or lesser fidelity to the initial text, as a model
for the teaching of elementary geometry. Each textbook
author has felt himself bound to respect the overall
division into Books, and within each book the disposition
and formulation of the different results or theorems, though
a certain number of more or less original commentaries were
appended as needed. In particular, relatively rarely did an
author add complementary figures covering specific cases
overlooked or ignored by Euclid.
One must never cease to
emphasize that the principal defect of the old proofs is
that they leave aside the relations of the situations,
and that these relations are often more difficult to
prove than the theorem which one has in view, to such an
extent that it is simpler to find a new proof than to
correct the old one. (B.M.E., 6, 1901, p. 132).
To establish the properties of a
parallelogram, we assume implicitly that two opposing
vertices are situated on opposite sides of the diagonal
which joins the other two vertices; the students would, I
believe, be quite embarassed if we asked them to give a
precise proof. (B.M.E., 6, 1901, p. 132)
Thus, in Proposition 20 of Book III, Euclid proves that
the magnitude of a central angle is twice that of the
corresponding inscribed angle (for any acute
inscribed angle), considering two cases:
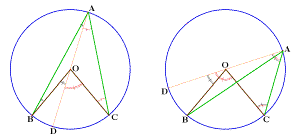
On the left, the point D
diametrically opposed to A is on
the "little" arc BC, on the right, it is on the "big" arc
BC
Certain commentators (from Clavius in the 16th century
until the end of the 19th century) add a third case of the
figure (point D is coincident with point B), but no word is
said of what might happen if the inscribed angle is
obtuse. In other words, while in the Elements
an angle can equally well be either acute or obtuse, when we
arrive at Proposition III, 20, a totally implicit
restriction is imposed, without apparently disturbing a soul
over the course of centuries.
Passing from thence to the theorem of the inscribed
quadrilateral (conditions under which four points may be on
a single circle), the authors content themselves in calling
on the notion of the arc of constant angle, or the equality
of two angles subtending the same arc. It is remarked of
course, in Euclid (III, 22), that the opposite angles of an
inscribed quadrilateral are supplementary (not
equal!), but on each occasion that the property of an
inscribed quadrilateral intervenes in the proof of a new
result, the proof is reasoned on the case of the figure
presented, without concern for that which would need to be
modified in another case, or even without concern as to
whether the case in question exists at all.
In elementary geometry,
one normally considers only the absolute value of angles,
without taking account of their direction, and without
distinguishing the original side from the terminal side.
This results in a multitude of complications. For
example, if A, B, C, and D are four points on a circle,
the angles ACB and ADB are supplementary or equal
depending on whether the points C and D are on opposite
sides of AB or not. By the same token, two angles of
which the sides are parallel or perpendicular are
sometimes equal, sometimes perpendicular. Therefore, in
the questions in which angles of this nature intervene,
one should review all of the possible cases; almost
always, these are ignored, and people content themselves
with examining the case of the figure in front of
them. (B.M.E., 1, 1895, p. 1).
The consideration of the ray,
or, which comes to the same thing, of direction on a
line, is necessary only if we need to take account of the
segments on that line; in all other cases, it creates an
embarassment, which disappears if one attributes a new
quality, the direction, to the angle formed by two lines:
that is, we distinguish one side of the angle from the
other. And in this case we have only one line, instead of
two, which forms a given angle with a given line; the
distinction between symmetry with respect to a point and
symmetry with respect to a line on a plane makes itself
clear; the set of points from which one sees a line
segment under a given angle is no longer composed of two
arcs of circumference, but rather of a single entire
circumference, a result more consistent with calculation,
and as a result the narrow and outdated concept of a line
segment capable of a given angle disappears. The authors
[B. Niewenglowski and L. Gérard] give
simultaneously the necessary and sufficient condition,
independent of the particular form of the figure, for
four points on a single circumference. (C. Michel,
B.M.E., 5, 1900, p. 93).
It seems that it is in the Géométrie
of J. Hadamard (1897) that the theorem on the inscribable
quadrilateral is given in the now classic necessary and
sufficient form:
If four points A, B, C, and D are on the a
single circumference, the angles in the same direction
formed by the lines AC and AD on the one hand, and BC and
BD on the other, are equal (and reciprocally) (Hadamard,
Géometrie plane, 1897, pp. 71-72).
This text lacks only the notation (AC, AD) (used by L.
Gérard) and an enumeration of the properties of the
oriented angle between two lines (Chasles relation, passage
to the opposite, etc...) for this notion to be usable in the
solution of problems in geometry.
The example of the proof
of the so-called property "of Simson's
line".
A property of elementary geometry resulting from the
property of the inscribed quadrilateral figures as an
example of application or as and exercise in every textbook
or course in geometry of the 19th century (and also of the
following century...). Here is its statement:
If one considers a point M
on a circle circumscribed around a triangle ABC, the
orthogonal projections of M on the three sides of the
triangle are colinear (following a line known as Simson's
Line).
This property apppears to be due not to Simson, but to
Wallace; nonetheless, despite efforts to promote the
appellation "Wallace's Line" (see for example
Intermédiaires des Mathématiciens, 1894
and 1895), both older and modern manuals speak entirely of
Simson's line. Numerous properties of elementary geometry
using Simson's line have been discovered over the course of
time, forming if you will a veritable chapter in the
geometry of the triangle. No matter the provenance, this
property was popularized at the beginning of the 19th
century. Below follows a classic proof, which appears to
orignate with Duhamel (around 1840):
The Simson's line
theorem (classical proof
(Duhamel?))
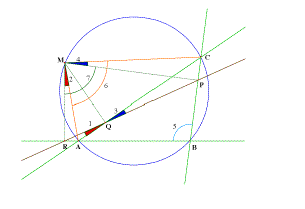
Angle 1: AQR Angle 2:
AMR Angle 3: CQP Angle 4: CMP
Angle 5: ABC Angle 6:AMC Angle 7: RMP
Proof:
1) The quadrilateral AMQR is inscribable: angles 1
and 2 are equal.
2) The quadrilateral CMPQ is inscribable: angles 3 and 4 are
equal.
3) The quadrilateral ABCM is inscribable: angles 5 and 6 are
supplementary.
4) The quadrilateral BMPR is inscribable: angles 5 and 7 are
supplementary.
5) From 3) and 4), angles 6 and 7 are equal.
6) It can be said that the angle CMR is equal to 2 + 6, and
also to 4 + 7.
7) From 5) and 6), angles 2 and 4 are equal.
8) From 1) and 2), angles 1 and 3 are equal.
9) As 1 and 3 are vertical angles, points P, Q and R are
colinear.
All of our books, all of
our professors in their courses think themselves obliged
to reproduce, as a model of analysis or of synthesis, the
classic proof (owed, I believe, to Duhamel) of the
theorem concerning Simson's Line; this proof is far from
simple, and, in the form in which it is presented, it
proves nothing. (B.M.E., 4, 1899, p. 273).
Such a reasoning is only valid
for the case of the specific figure, and it is also
possible that this case cannot appear, if the figure is
improperly drawn. In any case, to be rigorous, one should
begin by finding all of the possible figures, which would
seem inconvenient in the present case. (B.M.E., 4,
1899, p. 293).
Many readers have written me
that the classic proof is doubtless incomplete, but that
one feels that in the other cases of the figure, one
could create an analogous proof, and that should suffice.
This is an error: if one wishes to render the classic
proof rigorous, the difficulty consists precisely of
finding all of the possible cases of the figure.
(B.M.E., 4, 1899, p. 273).
If one does in fact attempt to determine which are the
possible configurations (of which only one serves as a
support to the classic proof), one is brought to the
consideration of the following figures. For each of them,
the proof must be modified (supplementary angles in the
place of equal angles, coincident or opposed points,
etc...)
Configurations de
Simson
Move the point M to explore all the
Simson's configurations on this
Cabri-Java construction of the famous figure.
(For more information about the Cabri-Java project contact
Gilles
Kuntz)
To get the static presentation of all the
Simson's configurations, click here :
In addition, the sums of angles, considered in item 6 of
the classic proof, must sometimes be replaced by
differences, or in any case be submitted to the classical
restriction: the sum of two angles cannot, if we wish still
to speak of angles, be more than two straight lines
(Euclid's definition of an angle). Equally, the differences
must not lead to negative angles, which implies that in a
figure where we can see that angle B is less than
angle A (and in which we intend to consider the difference
A-B), it is necessary to prove precisely that in this
case of the figure, we do indeed have B<A. And this is
applicable of course to every aspect of each case of the
figure.
L. Gérard gives two mathematical proofs of the
Simson property, based on the theorem of the inscribable
quadrilateral formulated in terms of oriented angles (and
therefore independent of the case of the figure
considered). The first is calculated on the classic proof,
the second is even more simple:
A - Adaptation of the "classical"
proof: (cf. the preceding figure)
The quadrilateral AMQR is inscribable: (AC, QR) =
(QA, QR) = (MA, MR).
The quadrilateral CMPQ is inscribable: (AC, QP) = (QC, QP) =
MC, MP).
The quadrilateral ABCM is inscribable: (BA, BC) = (MA,
MC).
The quadrilateral BMPR is inscribable: (MR, MP) = (BR, BP) =
(BA, BC).
(MR, MC) = (MR, MA) + (MA, MC) = -(AC, QR) + (BA, BC).
(MR, MC) = (MR, MP) + (MP, MC) = (BA, BC) - (AC, QP).
(AC, QR) = (AC, QP).
Points Q, P and R are colinear.
B - A more simple proof:
The quadrilateral AMQR is inscribable: (AM, AB) =
(AM, AR) = (QM, QR).
The quadrilateral CMPQ is inscribable: (CM, CB) = (CM, CP) =
(QM, QP).
The quadrilateral ABCM is inscribable: (AM, AB) = (CM,
CB).
(QM, QR) = (QM, QP)
Points Q, P and R are colinear.
This proof would appear
more complicated than the ordinary proof, where we
measure the angles by the arcs of circles; it is,
however, incomparably more simple, for to arrive at a
measurement of the angles, one must first distinguish the
different possible cases of the figure and, I repeat,
even in holding to the case of the figure that is before
one's eyes, one must prove that this case is possible:
otherwise one may easily prove anything one wishes. It is
in this manner that one can establish, by a well-known
reasoning, that an acute angle is equal to an obtuse
angle. (B.M.E., 4, 1899, p. 293).
Other mathematical proofs, that one may consider more
modern, are possible, using for example the properties of
similarity, but fundamentally it is always the theorem of
the inscribed quadrilateral that is at the origin of the
proof.
C - A proof based on
similarities:
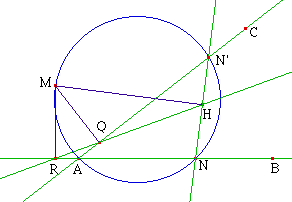
Let M be a point on a plane. There exists a unique
transformation ƒ, preserving similarities (in
French: "une similitude"), with center M which will map
AB to AC. The image of a point N on AB through this
transformation is the point N', the intersection of AC
and a circle passing through A, M and N.
Let H be the orthagonal projection of M
on NN'; the triangle MNH remains similar to itself when N
moves, so H describes a line (d) arrived at from AB by a
certain similitude. Two points on this line are in
fact known, points Q (when N is coincident with A) and R
(when N' is coincident with A). The line (d) is therefore
the line QR.
If M is on the circle circumscribed
about ABC, C is the image of B by ƒ and point H is
coincident with P, the orthagonal projection of M onto
BC.
Points P, Q and R are therefore
colinear.
Let us leave the final word once more to L.
Gérard:
When we compare two
proofs, one general and the other depending on a single
case of the figure, we are inclined to find the second
more clear than the first; but after some thought, we
perceive that the expressions, the details that appeared
obscure or bizarre in the general proof are necessary to
embrace this or that case to which we had not at first
paid attention. (B.M.E., 4, 1899, p. 273).
Reactions?
Remarks?
The reactions to the contribution of Michel Guillerault
will be
published in the November/December Proof Newsletter
©
Michel Guillerault 1998
Free translation: Virginia
Warfield
|

