O fortalecimento das demonstrações em
geometria elementar na virada do século XX

No fim do século XIX e início do século XX, desde M.Pasch e sobretudo depois D.Hilbert (Grundlagen der Geometrie, 1899), há uma preocupação de se estabelecer a geometria elementar sobre bases sólidas, não fazendo mais, implicitamente, referência aos casos de figuras particulares que possam se apresentar.
   Apresentamos aqui a contribuição a este debate de um relativamente modesto professor de classes preparatórias às Grandes Escolas francesas, parecendo-nos bastante esquecido nos nossos dias, Louis gérard, professor em Lyon e depois em Paris, especialista em geometria não euclideana (tese, 1892) e bastante preocupado em apresentar os teoremas da geometria elementar de uma maneira a mais rigorosa possível. Redator do Bulletin de Sciences mathématiques et physiques, publicou numerosas notas sobre o assunto e é autor (com a exceção de uma só) de todas as citações que irão se seguir. Em particular, ele é o promotor infatigável da noção de ângulos orientados de retas, noção que permite dar a numerosas proposições de geometria um caráter absolutamente geral, independente do caso da figura considerada.

Durante séculos, a obra de Euclides serviu, com uma certa fidelidade ao seu texto inicial, de modelo para o ensino da geometria elementar. Cada autor de manual respeitava a divisão geral em livros, e no interior de cada livro, a disposição e a formulação dos diferentes resultados ou teoremas, mesmo se comentários mais ou menos originais pudessem, se houvesse ocasião, ser acrescentados ao texto. Em particular, eram relativamente raros os autores que se permitiam acrescentar complementos, abrangendo casos de figuras esquecidas ou negligenciadas por Euclides.

"Não podemos deixar de repetir que a principal falha das demonstrações seculares é que elas deixam de lado as relações de situação e que estas relações são na maioria das vezes mais difíceis de se demonstrar que o teorema que se tem em vista , de maneira que é mais fácil achar uma nova demonstração do que corrigir a antiga." (B.M.E., 6, 1901, p. 132).

"Para estabelecer as propriedades do paralelogramo, admite-se implicitamente que dois vértices opostos estão situados de um lado e do outro da diagonal que liga os outros dois vértices; os alunos se sentiriam bastante embaraçados se lhes pedíssemos por dar em uma demonstração precisa" (B.M.E., 6, 1901, p.132).

É desta forma, que na proposição 20 do livro III, Euclides demonstra que o ângulo central é o dobro do ângulo inscrito correspondente (para um ângulo inscrito agudo), considerando dois casos: 

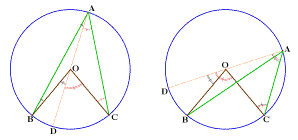
Na figura à esquerda, o ponto D diametralmente oposto a A é sobre o arco menor BC,
na figura à direita, ele está sobre o arco maior BC.

 

Certos comentaristas (de Clavius do século XVI até o fim do século XIX) acrescentam um terceiro caso de figuras ( o ponto D é confundido com B ou C), mas nenhuma palavra é dita sobre o que pode se passar se o ângulo é obtuso. Em outras palavras, apesar de nos Elementos, um ângulo poder ser tanto agudo quanto obtuso, quando chegamos à proposição 20 do livro III, uma restrição totalmente implícita é de rigor, sem que isto parece embaraçar ninguém no fim do século.

Passando ao teorema do quadrilátero inscritível (condição para que quatro pontos estejam sobre uma mesma circunferência), os autores se contentam em fazer intervir a noção de arco capaz, ou de igualdade de dois ângulos subentendendo o mesmo arco. Nota-se claramente , desde Euclides (III,22), que os ângulos opostos de um quadrilátero inscrito são suplementares ( e não iguais), mas cada vez que, na demonstração de um resultado, intervém a propriedade do quadrilátero inscritível, raciocina-se sobre o caso da figura apresentado, sem a preocupação daquilo que deveria ser modificado num outro caso de figura, ou mesmo, sem se preocupar em demonstrar que o caso da figura apresentado existe realmente.

"Em geometria elementar, considera-se o valor absoluto dos ângulos sem levar em conta o sentido e sem distinguir o lado origem do lado extremidade. Disto resulta uma série de complicações. Por exemplo: se A,B,C,D são quatro pontos de uma mesma circunferência, os ângulos ACB e ADB são suplementares ou iguais, de acordo com a posição dos pontos C e D de um lado ou do outro lado de AB. Do mesmo modo, dois ângulos de lados paralelos ou perpendiculares são iguais ou suplementares. Portanto, nas questões onde intervêm ângulos desta natureza, deve-se olhar todos os casos possíveis; costuma-se quase sempre dispensar este procedimento contentando-se em examinar o caso da figura que temos sob os olhos". (B.M.E., 1, 1895, p. 1).

"A consideração da semi-reta, ou, o que dá na mesma, do sentido da reta, é necessária, se precisarmos contar segmentos sobre esta reta; em todos os outros casos, ela cria um embaraço que desaparece quando se atribui ao ângulo de duas retas inteiras uma qualidade nova, o sentido, isto quer dizer se se distingue um do outro os dois lados do ângulo. E assim não há que uma só direção da reta, em vez de duas, que faz com uma reta dada um ângulo dado; a distinção entre a simetria em relação a um ponto e a simetria em relação a uma reta de um plano se torna precisa; o lugar geométrico dos pontos dos quais se vê um segmento de reta sob um ângulo dado se compõe, não mais de dois arcos de circunferência, mas de uma circunferência inteira, resultado mais de acordo com o cálculo, e, em seguida desaparece a idéia estreita e obsoleta de segmento capaz de um ângulo dado . Os autores ( B. Niewenglowski, et L.Gérard) dão ao mesmo tempo a condição necessária e suficiente, independente das formas particulares da figura, para que quatro pontos estejam sobre uma mesma circunferência" (C. Michel, B.M.E., 5, 1900, p. 93).

Parece que é na Géométrie de J. Hadamard (1897) que o teorema sobre o quadrilátero inscritível é dado sob a forma necessária e suficiente agora clássica

"Se os quatro pontos A,B,C,D estão sobre uma circunferência, os ângulos de mesmo sentido formados pelas retas AC, AD de um lado e BC e BD do outro, são iguais (e reciprocamente)" (Hadamard, Géométrie plane, 1897, pp. 71-72).

Faltam neste texto a notação (AC, AD) (usada por L.Gérard) e uma enumeração das propriedades do ângulo orientado de retas ( relação de Chasles, passagem ao oposto, etc...) para que se use esta noção na resolução de problemas de geometria.

O exemplo da demonstração da propriedade chamada "reta de Simson"

Uma propriedade da geometria elementar, que é consequência da propriedade do quadrilátero inscritível, surge como exemplo de aplicação ou como exercício, na totalidade dos manuais ou cursos de geometria do século XIX ( e também do século seguinte...)

Se se considera um ponto M da circunferência circunscrita a um triângulo ABC, as projeções ortogonais do ponto M sobre os três lados do triângulo são três pontos alinhados (seguindo uma reta chamada reta de Simson)

Esta propriedade não parece ser devida a Simson, mas a Wallace; entretanto, apesar dos esforços para promover o nome "reta de Wallace"(ver por exemplo Intermédiaire des Mathématiciens, anos 1894 e 1895), os manuais antigos ou modernos falam todos da reta de Simson. Numerosas propriedades da geometria elementar, utilizando a reta de Simson foram descobertas com o passar do tempo, formando um verdadeiro capítulo da geometria do triângulo. O que quer que seja, esta propriedade foi popularizada no início do século XIX. Veremos por exemplo uma demonstração clássica, que parece ser devida a Duhamel ( por volta de 1840):

 

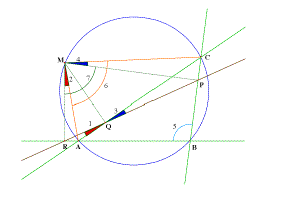
Ángulo 1: AQR Ángulo 2: AMR Ángulo 3: CQP Ángulo 4: CMP
Ángulo 5: ABC Ángulo 6:AMC Ángulo 7: RMP

Demonstração:

"Todas as nossas obras, todos os nossos professores, nos seus cursos, se acham obrigados a reproduzir, como um modelo de análise ou de síntese, a demonstração clássica (devida, creio, a Duhamel) do teorema relativo à reta de Simson; esta demonstração é longe de ser simples, e tal como é apresentada, ela não prova nada." ( (B.M.E., 4, 1899, p. 273).

"Um similar raciocínio é válido somente para o caso da figura considerada, e ainda pode acontecer que este caso não possa se apresentar, se a figura que é traçada for falsa. Em todos os casos, para ser rigoroso, seria necessário começar a procurar todos os casos possíveis de figuras, o que não parece cômodo, no caso atual." ( (B.M.E., 4, 1899, p. 293).

"Diversos leitores me escrevem dizendo que a demonstração clássica é sem dúvida incompleta , mas que se sente , que no caso de outras figuras, pode-se fazer uma demonstração análoga e que isto basta. Existe aí um erro, se quisermos tornar rigorosa a demonstração clássica, a dificuldade consiste precisamente em descobrir todos os casos possíveis de figura." (B.M.E., 4, 1899, p. 273).

Ora, se procuramos efetivamente quais são as configurações possíveis (donde somente uma serve de apoio à demonstração clássica) somos levados à consideração das figuras seguintes. Para cada uma delas, a demonstração deve ser modificada (ângulos suplementares em vez de serem iguais, coincidentes ou opostos pelo vértice, etc...)

Configurações de Simson

Além disso, as somas dos ângulos, consideradas no item 6 da demonstração clássica, devem ser, às vezes, substituídas por diferenças, ou de qualquer maneira devem ser submetidas à restrição clássica: a soma de dois ângulos não pode, se queremos ainda falar de ângulos, ser superior a dois retos (definição de Euclides de ângulo). Da mesma forma as diferenças eventuais não devem conduzir a ângulos negativos, o que quer dizer que numa figura onde se vê que o ângulo B é inferior ao ângulo A ( e que se considera em seguida a diferença A-B) deve-se demonstrar, precisamente , que neste caso da figura, tem-se B<A E isto se aplica sobre cada caso da figura.  

L.Gérard dá duas demonstrações da propriedade de Simson, baseadas sobre o teorema do quadrilátero inscritível enunciado em termos de ângulos orientados de retas ( e portanto independentes do caso da figura considerada). A primeira é calcada sobre a demonstração clássica, a segunda é ainda mais simples:

A- Adaptação da demonstração "clássica" (cf. figura precedente)

B- Uma demonstração mais simples

"Esta demonstração parece mais complicada que a demonstração comum, onde se medem os ângulos por arcos de circunferências; ela é, ao contrário, incomparavelmente mais simples, pois, para conseguir medir os ângulos, é preciso inicialmente distinguir os diversos casos de figuras possíveis e, repito, mesmo se limitando ao caso da figura que está sob os olhos, faltaria demonstrar que este caso é possível: caso contrário pode-se demonstrar tudo aquilo que se deseja. É assim que se demonstra por um raciocínio bem conhecido que um ângulo agudo é igual a um ângulo obtuso." (B.M.E., 4, 1899, p. 293).

Outras demonstrações, mais modernas, são possíveis, utilizando, por exemplo, as propriedades de semelhança, mas fundamentalmente é sempre o teorema do quadrilátero inscritível que é à origem da demonstração.

C- Uma demonstração utilizando a semelhança.

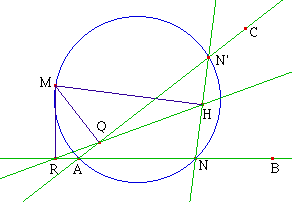
Seja M um ponto do plano. Existe uma única semelhança f de centro M fazendo passar de AB a AC. A imagem de um ponto N qualquer de AB por esta semelhança é o ponto N', intersecção de AC e da circunferência passando por A, M e N.
   Seja H a projeção ortogonal de M sobre NN'; o triângulo MNH permanece semelhante a si mesmo quando N varia, portanto H descreve uma reta (d) deduzida de AB por uma certa semelhança . Conhece-se de fato dois pontos dessa reta, os pontos Q (quando N está em A) e R (quando N' está em A). A reta (d) é portanto a reta QR
   Se M está sobre a circunferência circunscrita à ABC, C é o transformado de B pela semelhança f e o ponto H está em P, projeção ortogonal de M sobre BC. Os pontos P, Q, R são então alinhados.

Deixemos a palavra final mais uma vez a L.Gérard:

"Quando se comparam duas demonstrações, uma geral e a outra relativa a um só caso de figura, somos inclinados a achar que a segunda é mais clara que a primeira; mas após refletir, percebe-se que as expressões, os detalhes que pareciam obscuros ou bizarros na demonstração geral são necessários para abranger este ou aquele caso, o qual não se havia prestado atenção inicialmente." (B.M.E., 4, 1899, p. 273).

Volta a la carta