L'affermissement des
démonstrations en
géométrie élémentaire au
tournant du XXème siècle
par
Michel Guillerault
Laboratoire Leibniz
Grenoble - France
Vers la fin du XIXème siècle et au
début du XXème siècle, dès M.
Pasch et surtout après D. Hilbert (Grundlagen der
Geometrie, 1899), on se préoccupe
d'établir la géométrie
élémentaire sur des bases solides, ne faisant
plus implicitement référence aux cas de
figures particuliers qui peuvent se présenter.
On présente ici la contribution
à ce débat d'un relativement modeste
professeur de classes préparatoires aux Grandes
Écoles françaises, semble-t-il fort
oublié de nos jours, Louis Gérard, professeur
à Lyon puis à Paris, spécialiste de
géométrie non-euclidienne (Thèse, 1892)
et fort soucieux de présenter les
théorèmes de géométrie
élémentaire de la manière la plus
rigoureuse possible. Rédacteur du Bulletin de
Sciences mathématiques et physiques , il y a
publié de très nombreuses notes à ce
sujet et il est l'auteur (à l'exception d'une seule)
de toutes les citations qui vont suivre. En particulier , il
est le promoteur infatigable de la notion d'angles
orientés de droites, notion qui permet de donner
à de nombreuses propositions de
géométrie un caractère absolument
général, indépendant du cas de figure
considéré.
Pendant des siècles, l'œuvre d'Euclide a
servi, avec plus ou moins de fidélité au texte
initial, de modèle pour l'enseignement de la
géométrie élémentaire. Chaque
auteur de manuel se sentait tenu de respecter la division
générale en Livres, et à
l'intérieur de chaque livre, la disposition et la
formulation des différents résultats ou
théorèmes, même si des commentaires plus
ou moins originaux pouvaient, le cas échéant,
s'ajouter au texte. En particulier, relativement rares
étaient les auteurs qui se permettaient d'ajouter des
compléments embrassant des cas de figures
oubliés ou négligés par Euclide.
"Il
ne faut pas se lasser de répéter que le
principal défaut des démonstrations
séculaires, c'est qu'elles laissent de
côté les relations de situation et que ces
relations sont souvent plus difficiles à
démontrer que le théorème qu'on a en
vue, de sorte qu'il est plus facile de trouver une
nouvelle démonstration que de corriger
l'ancienne" (B.M.E.,
6, 1901, p. 132).
"Pour
établir les propriétés du
parallélogramme, on admet implicitement que deux
sommets opposés sont situés de part et
d'autre de la diagonale qui joint les deux autres
sommets; les élèves seraient, je crois,
fort embarrassés si on leur demandait d'en donner
une démonstration
précise"
(B.M.E., 6, 1901, p. 132).
C'est ainsi que dans la Proposition 20 du Livre III,
Euclide démontre que l'angle au centre est le double
de l'angle inscrit correspondant (pour un angle inscrit
aigu), en considérant deux cas :
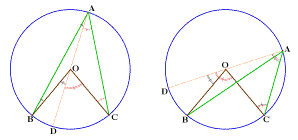
Dans la figure de gauche,
le point D diamétralement opposé à A
est sur
le "petit" arc BC, dans la figure de droite, il est sur le
"grand" arc BC
Certains commentateurs (de Clavius au XVIème
siècle jusqu'à la fin du XIXème
siècle) ajoutent un troisième cas de figure
(le point D confondu avec B ou C), mais aucun mot n'est dit
de ce qui peut se passer si l'angle inscrit est
obtus. Autrement dit, bien que dans les
Éléments, un angle puisse aussi bien
être aigu qu'obtus, lorsqu'on parvient à la
Proposition III, 20, une restriction totalement implicite
est de rigueur, sans que cela ne semble d'ailleurs
embarrasser personne au fil des siècles.
En passant de là au théorème sur le
quadrilatère inscriptible (conditions pour que quatre
points soient sur un même cercle), les auteurs se
contentent de faire intervenir la notion d'arc capable, ou
d'égalité de deux angles sous-tendant le
même arc. On remarque bien sûr, dès
Euclide (III, 22) que les angles opposés d'un
quadrilatère inscrit sont
supplémentaires (et non égaux!), mais
chaque fois que dans une démonstration d'un
résultat nouveau intervient la
propriété du quadrilatère inscriptible,
on raisonne sur le cas de figure présenté,
sans se soucier de ce qu'il faudrait modifier dans un autre
cas de figure, ou même, sans se préoccuper de
démontrer que la cas de figure présenté
existe vraiment.
"En
géométrie élémentaire, on ne
considère ordinairement que la valeur absolue des
angles, sans tenir compte du sens et sans distinguer le
côté origine du côté
extrémité. Il en résulte une
multitude de complications. Par exemple, si A, B, C, D
sont quatre points d'un même cercle, les angles
ACB, ADB sont supplémentaires ou égaux
selon que les points C et D sont ou non de part et
d'autre de AB. De même, deux angles dont les
côtés sont parallèles ou
perpendiculaires sont tantôt égaux,
tantôt supplémentaires. Donc, dans les
questions où interviennent des angles de cette
nature, il faudrait passer en revue tous les cas
possibles; on s'en dispense presque toujours et on se
contente d'examiner le cas de la figure qu'on a sous les
yeux" (B.M.E., 1, 1895, p. 1).
"La considération de la
demi-droite, ou, ce qui revient au même, du sens
sur une droite, n'est nécessaire que s'il y a lieu
de compter des segments sur cette droite; en tous autres
cas, elle crée un embarras, qui disparaît si
l'on attribue à l'angle de deux droites
entières une qualité nouvelle, le sens,
c'est-à-dire si l'on distingue l'un de l'autre les
deux côtés de l'angle. Et ainsi il n'y a
plus qu'une seule direction de droite, au lieu de deux,
qui fasse avec une droite donnée un angle
donné; la distinction entre la symétrie par
rapport à un point et la symétrie par
rapport à une droite d'un plan se précise;
le lieu des points d'où l'on voit un segment de
droite sous un angle donné se compose, non plus de
deux arcs de circonférence, mais d'une seule
circonférence tout entière, résultat
plus conforme au calcul, et , par suite disparaît
l'idée étroite et surannée de
segment capable d'un angle donné. Les auteurs
[B. Niewenglowski et L. Gérard] donnent en
même temps la condition nécessaire et
suffisante, indépendante des formes
particulières de la figure, pour que quatre points
soient sur une même circonférence."
(C. Michel, B.M.E., 5, 1900, p. 93).
Il semblerait que c'est dans la
Géométrie de J. Hadamard (1897) que le
théorème sur le quadrilatère
inscriptible est donné sous la forme
nécessaire et suffisante maintenant classique
"Si les quatre points A, B, C, D sont sur une
même circonférence, les angles de même
sens formés par les droites AC, AD d'une part, BC
et BD d'autre part, sont égaux (et
réciproquement)" (Hadamard,
Géométrie plane, 1897, pp. 71-72).
Il ne manque plus dans ce texte que la notation (AC, AD)
(utilisée par L. Gérard) et une
énumération des propriétés de
l'angle orienté de droites (relation de Chasles,
passage à l'opposé, etc...) pour que l'on
utilise cette notion dans la résolution des
problèmes de géométrie.
L'exemple de la
démonstration de la propriété dite "de
la droite de Simson"
Une propriété de géométrie
élémentaire conséquence de la
propriété du quadrilatère inscriptible
figure comme exemple d'application ou comme exercice dans la
totalité des manuels ou cours de
géométrie du XIXème siècle (et
aussi du siècle suivant...). En voici
l'énoncé:
Si on considère un
point M du cercle circonscrit à un triangle ABC,
les projections orthogonales du point M sur les trois
côtés du triangle sont trois points
alignés (suivant une droite appelée droite
de Simson).
Cette propriété ne semble pas due à
Simson, mais à Wallace; cependant, malgré des
efforts pour promouvoir l'appellation "droite de Wallace"
(voir par exemple Intermédiaire des
Mathématiciens, années 1894 et 1895), les
manuels anciens ou modernes parlent tous de la droite de
Simson. De nombreuses propriétés de
géométrie élémentaire utilisant
la droite de Simson ont été découvertes
au fil du temps, formant si l'on veut un véritable
chapitre de la géométrie du triangle. Quoi
qu'il en soit, cette propriété a
été popularisée au début du
XIXème siècle. En voici par exemple une
démonstration classique, qui semble due à
Duhamel (vers 1840):
Le
théorème de la droite de Simson
(démonstration classique
(Duhamel?))
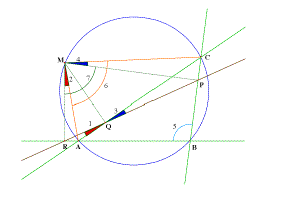
Angle 1: AQR Angle 2:
AMR Angle 3: CQP Angle 4: CMP
Angle 5: ABC Angle 6:AMC Angle 7: RMP
Démonstration:
1) Le quadrilatère AMQR est inscriptible: les
angles 1 et 2 sont égaux.
2) Le quadrilatère CMPQ est inscriptible: les angles
3 et 4 sont égaux.
3) Le quadrilatère ABCM est inscriptible: les angles
5 et 6 sont supplémentaires.
4) Le quadrilatère BMPR est inscriptible: les angles
5 et 7 sont supplémentaires.
5) D'après 3) et 4), les angles 6 et 7 sont
égaux.
6) On peut écrire que l'angle CMR est égal
à 2+6, et aussi à 4+7.
7) D'après 5) et 6), les angles 2 et 4 sont
égaux.
8) D'après 1) et 2), les angles 1 et 3 sont
égaux.
9) 1 et 3 étant opposés par le sommet, les
points P, Q, R sont alignés.
"Tous nos ouvrages, tous
nos professeurs dans leur cours se croient obligés
de reproduire, comme un modèle d'analyse ou de
synthèse, la démonstration classique (due,
je crois, à Duhamel) du théorème
relatif à la droite de Simson; cette
démonstration est loin d'être simple, et,
telle qu'elle est présentée, elle ne prouve
rien" (B.M.E., 4, 1899, p. 273).
"Un pareil raisonnement n'est
valable que pour le cas de figure
considéré, et encore il peut arriver que ce
cas ne puisse se présenter, si la figure qu'on a
tracée est fausse. En tous cas, pour être
rigoureux, il faudrait commencer par chercher tous les
cas de figure possibles, ce qui ne paraît pas
commode, dans le cas actuel" (B.M.E., 4, 1899, p.
293).
"Plusieurs lecteurs m'ont
écrit que la démonstration classique est
sans doute incomplète, mais qu'on sent, que dans
les autres cas de figure, on peut faire une
démonstration analogue et que cela suffit. Il y a
là une erreur; si l'on veut rendre rigoureuse la
démonstration classique, la difficulté
consiste précisément à trouver tous
les cas de figure possibles" (B.M.E., 4, 1899, p.
273).
Or, si l'on cherche effectivement quelles sont les
configurations possibles (dont seule l'une d'elles sert
d'appui à la démonstration classique), on est
amené à la considération des figures
suivantes. Pour chacune d'entre elles, la
démonstration est à modifier (angles
supplémentaires au lieu d'être égaux,
confondus ou opposés par le sommet, etc...)
Configurations de
Simson
Manipuler le point M pour explorer les
configurations de Simson sur cette
construction Cabri-Java de la fameuse figure.
(Contact pour le projet Cabri-Java : Gilles
Kuntz)
Pour voir l'image statique des
configurations de Simson, cliquer ici :
De plus, les sommes d'angles, considérées
à l'item 6 de la démonstration classique,
doivent être parfois remplacées par des
différences, ou en tout état de cause,
être soumises à la restriction classique: la
somme de deux angles ne peut, si on veut encore parler
d'angles, être supérieure à deux droits
(définition d'Euclide de l'angle). De même les
différences éventuelles ne doivent pas
conduire à des angles négatifs, ce qui veut
dire que dans une figure où l'on voit que l'angle B
est inférieur à l'angle A (et qu'on
considère ensuite la différence A-B), il faut
démontrer précisément que dans ce cas
de figure, on a bien B<A. Et ceci s'applique bien entendu
à tout ce qui est vu sur chaque cas de figure.
L. Gérard donne deux démonstrations de la
propriété de Simson, fondées sur le
théorème du quadrilatère inscriptible
énoncé en termes d'angles orientés de
droites (et donc indépendantes des cas de figure
considérés). La première est
calquée sur la démonstration classique, la
seconde est encore plus simple:
A - Adaptation de la
démonstration "classique": (cf. figure
précédente)
Le quadrilatère AMQR est inscriptible: (AC,
QR) = (QA, QR) = (MA, MR).
Le quadrilatère CMPQ est inscriptible: (AC, QP) =
(QC, QP) = (MC, MP).
Le quadrilatère ABCM est inscriptible: (BA, BC) =
(MA, MC).
Le quadrilatère BMPR est inscriptible: (MR, MP) =
(BR, BP) = (BA, BC).
(MR, MC) = (MR, MA) + (MA, MC) = - (AC, QR) + (BA, BC).
(MR, MC) = (MR, MP) + (MP, MC) = (BA, BC) - (AC, QP).
(AC, QR) = (AC, QP).
Les points Q, P, R sont alignés.
B - Une démonstration plus
simple:
Le quadrilatère AMQR est inscriptible: (AM,
AB) = (AM, AR) = (QM, QR)
Le quadrilatère CMPQ est inscriptible: (CM, CB) =
(CM, CP) = (QM, QP)
Le quadrilatère ABCM est inscriptible : (AM, AB) =
(CM, CB)
(QM, QR) = (QM, QP)
Les points Q, P, R sont alignés.
"Cette
démonstration paraîtra plus
compliquée que la démonstration ordinaire,
où l'on mesure les angles par des arcs de cercles;
elle est, au contraire, incomparablement plus simple,
car, pour arriver à mesurer les angles, il faut
d'abord distinguer les divers cas de figure possibles et,
je le répète, même en se bornant au
cas de figure qu'on a sous les yeux, il faudrait
démontrer que ce cas est possible: autrement on
arrive à démontrer tout ce qu'on veut.
C'est ainsi qu'on démontre, par un raisonnement
bien connu, qu'un angle aigu est égal à un
angle obtus." (B.M.E., 4, 1899, p. 293).
D'autres démonstrations, plus modernes si l'on
veut, sont possibles, utilisant par exemple les
propriétés des similitudes, mais
fondamentalement c'est toujours le théorème du
quadrilatère inscriptible qui est à l'origine
de la démonstration.
C - Une démonstration
utilisant les similitudes:
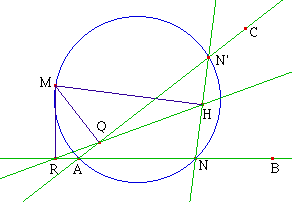
Soit M un point du plan. Il existe une
similitude unique f de centre M faisant passer de AB
à AC. L'image d'un point N quelconque de AB par
cette similitude est le point N', intersection de AC et
du cercle passant par A, M et N.
Soit H la projection orthogonale de M
sur NN'; le triangle MNH reste semblable à
lui-même quand N varie, donc H décrit une
droite (d) déduite de AB par une certaine
similitude. On connaît en fait deux points de cette
droite, les points Q (quand N est en A) et R (quand N'
est en A). La droite (d) est donc la droite QR.
Si M est sur le cercle circonscrit
à ABC, C est le transformé de B par la
similitude f et le point H est en P, projection
orthogonale de M sur BC. Les points P, Q, R sont alors
alignés.
Laissons le mot de la fin une fois encore à L.
Gérard:
"Quand on compare deux
démonstrations, l'une générale,
l'autre relative à un seul cas de figure, on est
enclin à trouver la seconde plus claire que la
première; mais après réflexion, on
s'aperçoit que les expressions, les détails
qui avaient paru obscurs ou bizarres dans la
démonstration générale sont
nécessaires pour embrasser tel ou tel cas auquel
on n'avait pas fait d'abord attention" (B.M.E., 4,
1899, p. 273).
Réactions?
Remarques?
Les réactions à la contribution de Michel
Guillerault seront
publiées dans la Lettre de la Preuve de
Novembre/Décembre
©
Michel Guillerault 1998
|

