Consolidación de la
Demostración en Geometría Elemental
en el Cambio al Siglo XX
Michel Guillerault
Laboratoire Leibniz
Grenoble - France
Desde el fin del siglo XIX y al principio del XX, desde
M. Pasch y sobre todo después de D. Hilbert (en
Grundlagen der Geometrie, 1899), existe la
preocupación de establecer la geometría sobre
bases sólidas, y de ya no hacer más
referencias implícitas a casos que pudieran
presentarse de figuras particulares.
En este artículo presentamos la
contribución a este debate de un profesor de clases
preparatorias a las "Grandes Écoles "
francesas: Louis Gérard, profesor relativamente
modesto, el cual al parecer actualmente se encuentra en el
olvido. L. Gérard fué profesor en Lyon y
después en Paris, especialista en geometría
no-euclidiana (Tesis, 1892), estuvo muy preocupado por
presentar los teoremas de geometría elemental de la
manera más rigurosa posible. En particular, L.
Gérard fué promotor infatigable de la
noción de ángulos entre rectas orientados,
noción que permite dar a numerosas proposiciones de
geometría un caracter absolutamente general,
independiente de los casos de figuras en
consideración. Gérard fue redactor del
Bulletin de Sciences Mathématiques et
Physiques, publicó numerosas notas al respecto y
es autor (con exepción de una sola) de todas las
citas que siguen a continuación.
Durante siglos, más o menos siendo fieles al texto
inicial, la obra de Euclides ha servido de modelo para la
enseñanza de la geometría elemental. Cada
autor de manual se sentía inclinado a respetar la
división general en Libros de Los Elementos, y al
interior de cada libro, la disposición y la
formulación de diferentes resultados o teoremas,
mismo si se daba el caso de agregar comentarios más o
menos originales al texto. En particular, eran relativamente
raros los autores que se permitían agregar
complementos que contenían casos de figuras olvidadas
o dejadas al margen por Euclides.
No hay que dejarse de
repetir que el principal defecto de las demostraciones
seculares es que dejan de lado las relaciones de
situación y que estas relaciones son
frecuentemente más difíciles a demostrar
que el teorema en cuestión, de manera que es
más facil encontrar una nueva demostración
que corregir la antigua. (B.M.E., 6, 1901, p.
132).
Para establecer las propiedades
del paralelogramo, se admite implícitamente que
dos vértices opuestos están situados uno en
una parte, y el otro en la otra, de la diagonal que une
los otros dos vértices; los estudiantes
estarían, yo creo, fuertemente impedidos si se les
pidiera dar una demostración precisa.
(B.M.E., 6, 1901, p. 132)
Es así como en la proposición 20 del Libro
III, Euclídes demuestra que el ángulo central
es el doble del ángulo inscrito correspondiente (para
un ángulo inscrito agudo), considerando dos
casos:
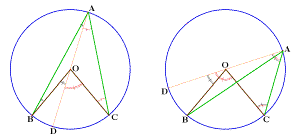
A la izquierda, el punto
D diametrálmente opuesto a A está sobre
el arco `pequeño´ BC, a la derecha, el punto D
está sobre el arco `grande´ BC.
Ciertos comentaristas (desde Clavius en el siglo XVI,
hasta el final del siglo XIX) agregan el caso de una tercera
figura (el punto D sobrepuesto en B o C), pero no se dice
ninguna palabra de lo que puede pasar si el ángulo
inscrito es obtuso. Dicho de otra manera, si bien en
los Elementos un ángulo bien puede ser tanto
águdo como obtuso, cuando se llega a la
proposición III, 20, es de rigor una
restricción totalmente implícita, sin que esto
parezca, por otro lado, causar dificultades a nadie al paso
de los siglos.
Pasando de ahí al teorema sobre el
cuadrilátero inscrito ( condiciones para que cuatro
puntos estén sobre un mismo círculo), los
autores se contentan de hacer intervenir la noción de
arco "capaz" (capable), o de igualdad de dos ángulos
que subtienden el mismo arco. Es de remarcar, por supuesto,
desde Euclídes (III, 22) que los ángulos
opuestos de un cuadrilátero inscrito sean
suplementarios (¡y no iguales!), pero cada vez
que en una demostración de un resultado nuevo
interviene la propiedad del cuadrilátero inscrito, se
razona sobre el caso de la figura presentada, sin
preocuparse de que sería necesario modificar en el
caso de otra figura, o mismo, sin preocuparse de demostrar
que el caso de la figura presentada existe
verdaderamente.
En geometría
elemental, no se considera ordinariamente más que
el valor absoluto de los ángulos, sin tener en
cuenta el sentido y sin distinguir el lado orígen
del lado extremo. Resultan una multitud de
complicaciones. Por ejemplo, si A, B, C, D son cuatro
puntos de un mismo círculo, los ángulos
ACB, ADB son suplementarios o iguales según que
los puntos C y D sean o no de una parte o de la otra de
AB. Así mismo, dos ángulos cuyos lados son
paralelos o perpendiculares son ya sea iguales, ya sea
suplementarios. Luego, en las cuestiones donde
intervienen ángulos de esta naturaleza,
sería necesario pasar revista a todos los casos
posibles; esto se dispensa casi siempre y uno se contenta
de examinar el caso de la figura que se tiene bajo los
ojos. (B.M.E., 1, 1895, p. 1).
La consideración de la
semirecta, o lo que viene a ser lo mismo, del sentido
sobre una recta, es necesario solamente cuando hay que
contar segmentos sobre esta recta; en todos los otros
casos, esta consideración crea una dificultad que
desaparece si se le atribuye al ángulo entre dos
rectas enteras una cualidad nueva: el sentido, es decir,
si se distinguen el uno del otro los dos lados del
ángulo. Y así no hay más que una
sola dirección de la recta, en lugar de dos, que
hace con una recta dada un ángulo dado; la
distinción entre la simetría en
relación a un punto y la simetría en
relación a una recta de un plano se precisa; el
lugar de los puntos desde donde se ve un segmento de
recta bajo un ángulo dado se compone ya no de dos
arcos de circunferencia, sino de una sola circunferencia
completa, resultado más conforme al
cálculo, y, en seguida (o en consecuencia)
desaparece la idea estrecha de segmento "capaz" de un
ángulo dado. Los autores (B. Niewenglowski y
L.Gerard) dan al mismo tiempo la condición
necesaria y suficiente, independiente de las formas
particulares de la figura, para que cuatro puntos esten
sobre una misma circunferencia. (C. Michel,
B.M.E., 5, 1900, p. 93).
Parecería que es en la
Géométrie de J.Hadamard (1897) que el
teorema sobre el cuadrilátero inscrito está
dado bajo la forma necesaria y suficiente ahora
clásica:
Si los cuatro puntos A, B, C, D están
sobre una misma circunferencia, los ángulos de
mismo sentido formados por las rectas AC, AD de un lado,
BC y BD de la otra parte, son iguales (y
recíprocamente) (Hadamard,
Géométrie plane, 1897, pp.71-72).
En este texto no hace falta nada más que la
notación (AC, AD) (utilizada por L. Gérard) y
una enumeración de las propiedades de ángulo
orientado entre rectas (relación de Chasles, pasaje
al opuesto, etc....) para que se utilice esta noción
en la resolución de problemas de
geometría.
Ejemplo de la
Demostración de la Propiedad llamada "de la Recta de
Simson".
Una propiedad de geometría elemental consecuencia
de la propiedad del cuadrilátero inscrito figura como
ejemplo de aplicación o como ejercicio en la
totalidad de manuales o cursos de geometría del siglo
XIX (y también del siglo siguiente...). He
aquí el enunciado:
Si se considera un punto M
del círculo circunscrito a un triángulo
ABC, las proyecciones ortogonales del punto M sobre los
tres lados del triángulo son tres puntos alineados
(siguiendo una recta llamada recta de Simson).
Esta propiedad no parece debida a Simson, sino a Wallace;
sin embargo a pesar de los esfuerzos para promover la
apelación "recta de Wallace" (ver, por ejemplo,
Intermédiaires des Mathématiciens,
años 1894 y 1895), los manuales antigüos o
modernos hablan todos de la recta de Simson. Numerosas
propiedades de geometría elemental utilizando la
recta de Simson han sido descubiertas a lo largo de los
años, formando si se quiere un verdadero
capítulo de la geometría del triángulo.
De cualquier manera, esta propiedad ha sido popularizada a
principios del siglo XIX. He aquí por ejemplo una
demostración clásica, que parece debida a
Duhamel (hacia 1840):
Teorema de la Recta de
Simson (Demostración Clásica
(Duhamel?))
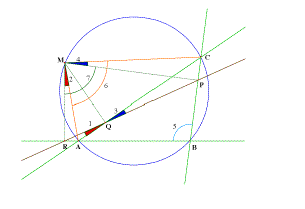
Ángulo
1: AQR Ángulo 2:
AMR Ángulo 3: CQP Ángulo 4: CMP
Ángulo 5: ABC Ángulo 6:AMC Ángulo 7:
RMP
Demostración:
1) El cuadrilátero AMQR es inscrito: los
ángulos 1 y 2 son iguales.
2) El cuadrilátero CMPQ es inscrito: los
ángulos 3 y 4 son iguales.
3) El cuadrilátero ABCM es inscrito: los
ángulos 5 y 6 son suplementarios.
4)El cuadrilátero BMPR es inscrito: los
ángulos 5 y 7 son suplementarios.
5) De 3) y 4), los ángulos 6 y 7 son iguales.
6) Se puede escribir que el ángulo CMR es igual a
2+6, y también a 4+7.
7) De 5) y 6), los ángulos 2 y 4 son iguales.
8) De 1) y 2), los ángulos 1 y 3 son iguales.
9) 1 y 3 siendo opuestos por el vértice, los puntos
P, Q, R están alineados.
Todas nuestras obras,
todos nuestros profesores en sus cursos, se creen
obligados a reproducir, como modelo de análisis o
de síntesis la demostración clásica
(debida, yo creo, a Duhamel) del teorema relativo a la
recta de Simson; esta demostración está
lejos de ser simple, y tal cual está presentada,
no prueba nada. (B.M.E., 4, 1899, p. 273).
Un razonamiento parecido es
válido sólo para el caso de la figura
considerada, y aún puede suceder que este caso
pueda no presentarse si la figura que se ha trazado es
falsa. En todos los casos, para ser rigurosos,
sería necesario comenzar por buscar todos los
casos de figuras posibles, lo que no parece cómodo
en el caso actual. (B.M.E., 4, 1899, p. 293).
Muchos lectores me han escrito
que la demostración clásica está sin
duda incompleta, pero que "se siente" que en los casos de
otras figuras se puede hacer una demostración
análoga y que ello es suficiente. Ahí hay
un error; si se quiere reforzar la demostración
clásica, la dificultad consiste precisamente en
encontrar todos los casos de figuras posibles.
(B.M.E., 4, 1899, p. 273).
Es decir que si se busca efectivamente cuáles son
las configuraciones posibles (en donde sólo una de
ellas sirve de apoyo a la demostración
clásica), hemos llegado a la consideración de
las figuras siguientes. Para cada una de ellas la
demostración se debe modificar (ángulos
suplementarios en lugar de ser iguales, sobrepuestos u
opuestos por el vértice, etc.,...).
Configurations de
Simson
Manipular el punto M, con el fin de
explorar las configuraciones de
Simson, en la construcción Cabri-Java de la figura ya
mencionada.
(Contacto para el proyecto Cabri-Java: Gilles
Kuntz )
Para ver la imagen estática de las
configuraciones de Simson, haga click aquí:

Además, las sumas de los ángulos
considerados en el item 6 de la demostración
clásica, deben ser algunas veces reeplazadas por
diferencias, o bajo cualquier consideración, ser
sometidas a la restricción clásica: la suma de
dos ángulos no puede, si se quiere aún hablar
de ángulos, ser superior a dos rectos
(definición de Euclides de ángulo).
Asímismo, las diferencias eventuales no deben
conducir a ángulos negativos, lo que quiere decir que
en una figura en donde se quiere que el ángulo B sea
inferior al ángulo A (y en donde se considera
enseguida la diferencia A-B), es necesario demostrar,
precisamente, que en la figura del caso, se tiene B<A. Y
esto se aplica, por supuesto, a todo lo que se ha visto
sobre cada caso de figura particular.
L. Gérard da dos demostraciones de la propiedad de
Simson, fundadas sobre el teorema del cuadrilátero
inscrito enunciado en términos de ángulos
orientados entre rectas (y entonces independientes de
los casos de las figuras en consideración). La
primera está calcada de la demostración
clásica, la segunda es aún más
simple:
A. Adaptación de la
demostración "clásica":(cf. figura
precedente)
El cuadrilátero AMQR es inscrito: (AC, QR) =
(QA, QR) = (MA, MR).
El cuadrilátero CMPQ es inscrito: (AC, QP) = (QC, QP)
= (MC, MP).
El cuadrilátero ABCM es inscrito: (BA, BC) = (MA,
MC).
El cuadrilátero BMPR es inscrito: (MR, MP) = (BR, BP)
= (BA, BC).
(MR, MC) = (MR, MA) + (MA, MC) = -(AC, QR) + (BA, BC).
(MR, MC) = (MR, MP) + (MP, MC) = (BA, BC) - (AC, QP).
(AC, QR) = (AC, QP).
Los puntos Q, P, R están alineados.
B. Una demostración
más simple:
El cuadrilátero AMQR es inscrito: (AM, AB) =
(AM, AR) = (QM, QR).
El cuadrilátero CMPQ es inscrito: (CM, CB) = (CM, CP)
= (QM, QP).
El cuadrilátero ABCM es inscrito: (AM, AB) = (CM,
CB).
(QM, QR) = (QM, QP)
Los puntos Q, P, R están alineados.
Esta demostración
parecerá más complicada que la
demostración ordinaria, en donde se miden los
ángulos por arcos de círculos; ella es, al
contrario,incomparablemente más simple, porque,
para llegar a medir ángulos, es necesario
distinguir los casos diversos de las figuras posibles y,
lo repito, aún restringiéndose al caso de
la figura que se tiene bajo los ojos, sería
necesario demostrar que este caso es posible: de otra
manera, se llega a demostrar todo lo que se quiera. Es
así que se demuestra, por un razonamiento muy
conocido, que un ángulo agudo es un ángulo
obtuso. (B.M.E., 4, 1899, p. 293).
Otras demostraciones son posibles, más modernas si
se quiere, utilizando por ejemplo las propiedades de
semejanza, sin embargo, fundamentalmente es siempre el
teorema del cuadrilátero inscrito el que está
en el orígen de la demostración.
C. Una demostración
utilizando semejanzas:
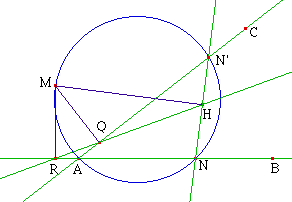
Sea M un punto del plano. Existe una semejanza
única f de centro M que hace pasar de AB a AC. La
imagen de un punto N cualquiera de AB por esta semejanza
es el punto N', intersección de AC y del
círculo que pasa por A, M y N.
Sea la proyección ortogonal de M
sobre NN´; el triángulo MNH queda semejante a
él mismo cuando N varía, luego H describe
una recta (d) deducida de AB por una cierta semejanza. Se
conocen de hecho dos puntos de esta recta, los puntos Q
(cuando N está en A) y R (cuando
N´está en A. La recta (d)es entonces la recta
QR.
Si M está sobre el
círculo circunscrito a ABC, C es el transformado
de B por la semejanza f y el punto H esta en P,
proyección ortogonal de M sobre BC.
Los puntos P, Q, R están
entonces alineados.
Dejemos la palabra final, una vez más, a L.
Gérard:
Cuando se comparan dos
demostraciones, una general y otra relativa al caso de
una sola figura, se está inclinado a encontrar la
segunda más clara que la primera; pero
después de reflexionar, se percibe que las
expresiones, los detalles que habían parecido
obscuros o raros en la demostración general son
necesarios para contemplar tal o cual caso, al cual no se
había puesto inicialmente atención.
(B.M.E., 4, 1899, p. 273).
¿Reacciones?,
¿Observaciones?
La contribución de Michel Guillerault sera
publicada en la carta de Octubre/Noviembre.
©
Michel Guillerault 1998
Traduciòn
Veronica Hoyos Aguilar
|

