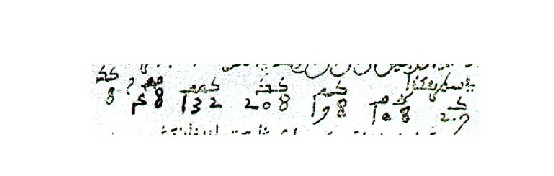La lettre de la Preuve

ISSN 1292-8763

 

Proof in Arabian Algebra

Arabian algebra developed starting in the eleventh century by constructing a science built on the types of calculation practiced by different people in everyday life (artisans, merchants, juridical consultants, scribes, calculators, astronomers,…) Its structure consisted of three types of knowledge: equations, irrationals and unknowns. These systems, whose premises were already found in the sciences of antiquity and also in Indian science, were built up at the same time, each with its own particular logic and its own methods but also intensely influenced by the other systems, constituting from the twelfth century on an autonomous body with its own specialists, Ahl al-Jabr (algebraists), its concepts, its types of reasoning, its stereotypes and of course its results. Research into the status of proof in Arabian algebra thus requires that we identify the types of proof specific to each system and in particular those which algebraists recognize as valid.

1.A typology of equations and their associated algorithms

When the caliph al-Ma'moun asked al-Quarismi (790-650) to produce the first treatise on Arabian algebra, he wanted to make available to users a tool which would synthesize the scattered knowledge concerning the resolution of problems of everyday life. Al-Quarismi's opuscule is very short, its announced objective being to codify a practice known among calculators: turning problems into equations and resolving linear and quadratic equations with positive whole or fractional coefficients. It identifies six canonical equations to which, in principle, all problems can be reduced and offers an algorithm for the solution of each of them. What is new about this work is not the algorithms themselves, some of which can be found among the Egyptians, others among the Babylonians and most among the Indians, but the author's desire to classify the canonical equations and to fix the vocabulary simultaneously for the mathematical objects: mãl (some goods), jidhr, (a root) and 'adãd (a given number), for relations and even for forms of reasoning. This vocabulary is familiar to any reader able to calculate with natural numbers or fractions, the operations: addition, subtraction, multiplication, division and extraction of the square root are common practice in arithmetic.
   The properties of commutativity and distibutivity can be seen by analogy with those on the whole numbers. As to the new pieces of reasoning, they are indeed described. The terms which designate them are included in the title itself of the work: Kitab al-Jabr wal-Muqabala, the first al-Jabr (restoration) refers to the operation of getting rid of the negative terms appearing in one of the members of the equation and the second term al-Muqabala (opposition) is the operation of reduction of similar terms, that is, those of the same degree.
   The algorithm for resolution of a canonical equation is stated starting with a generic example of a numerical equation with simple coefficients of which at least one root is positive and quasi-obvious. It is a sequence of stereotypical instructions:

• Take half of the number of jidhr
• Multiply it by itself
• Subtract from the result the 'adãd
• Take the square root of the result
• Subtract this result from half of the jidhr, you will find a first solution.
• Add the result to half of the jidhr, you will find a second solution.

These generic examples can be found also in the algebraic treatises of most of al-Khwarizmi's successors. A new term shay (a thing) is borrowed from everyday language, it corresponds to the thing sought for. It is used to identify in a problem the number that is to be determined using the given numbers. An equation thus becomes the putting into a binary relationship, by means of the equality, of three types of objects (which today we would call monomials) : things (shay), their products with themselves (mãl) and the numbers given in the statement of the problem ('adãd). The status of the unknown evolved rapidly; we will speak of it again in paragraph 4.
    The algorithms for resolving quadratic equations were completely standardized and were formulated symbolically by the Magrebian algebraists (but only by them) by the 13th century. Symbolic language used in heuristic reasoning (today we would say in calculations on scratch paper) before being translated into the language of rhetoric necessary for the communication of results. In certain algebraic writings, like that of al-Qalasadi (1412-1486), the Maghrebian symbols even replace their rhetorical equivalent. The following example illustrates perfectly this slippage from stereotypical reasoning to symbolic notation:

The logical sequence of reasoning translates to a sequence of equations of intermediate results, each occupying one line and in order from top to bottom, without the use of logical connectors. The rules are implicit, but visible.

Third degree equations

The typology of quadratic equations was extended to third degree equations by Omar al-Khayyam (1048-1131) and by Sharaf ad-Din at-Tusi (1135-1213) who, not succeeding in finding solutions to them by radicals, tried to find them geometrically. We will discuss their approach in paragraph 3.

2. The arithmetic of irrational numbers

Although al-Khwarizmi used only natural numbers and fractions as coefficients in the canonical equations he treated, his immediate successors like Abu Kamil (850 - 930) and later ones like al-Karaji (953 - 1028) extended algebraic calculations to equations whose coefficients could be irrational. The arithmetic of irrationals, which was embryonically present with al-Khwarizmi, became an autonomous chapter preliminary to any theory of equations. The toolbox is explicitly Euclidean, containing chapter X of Euclid's Elements, the reasoning and verification being geometric.
Two evolutions can meanwhile be observed: on the one hand, the naturalization of calculation on radicals leaving aside geometric justifications and on the other the invention by the Maghrebians of a symbolism specific to radicals similar to algebraic symbolism. From then on one could reason on radicals as one reasons on numbers by applying the properties of commutativity and distributivity of irrational numbers.

3. Geometric proofs

What distinguishes al-Khwarizmi from his predecessors in antiquity or in India is his concern for justifying the algorithms for solving quadratic equations. "I have described," he writes, "the exact algorithms of solution [for these equations] and I have established for each one a diagram which makes it possible to deduce the justification [of the result.]" This portion of al-Khwarizmi's treatise is of no value for calculations, but makes it possible to demonstrate that the work is scientific, in the sense that its mathematical objects have been defined and the consequent properties demonstrated. Nonetheless, his proofs are pragmatic. They are based on diagrams which are to be kept in sight and followed step by step while describing in everyday language the steps of the reasoning. Addition of figures to the original diagram, of subtraction of them from it, application of areas or respecting the homogeneity of the terms on which on it is operating are indeed Euclidean practices (cf. Arsac, 1999), but references to Euclid are non-existent and his direct influence never acknowledged.
   Finally we note that al-Khwarizme justifies the algorithms for solving quadratic equations whose coefficients are particular whole natural number. These equations are considered to be generic examples and were taken up again by most of his successors, even those who adopted new proofs.
   The pragmatic proofs presented by al-Khwarizmi and based on a direct reading of diagrams satisfied neither the community of geometers nor the nascent one of algebraists, the former considering that all reasoning should be based explicitly on Euclid's Elements and the latter wishing to escape its tutelage. Thabit ibn Qurra (826-900) was among the former, while al-Karaji, although he systematically adopted their process, created the conditions for the Euclidean formalism to be blurred, and can be considered as the real inventor of algebra as an established science, with its own definitions, identified propositions and original proofs.

Euclidean proofs

A specialist in Greek mathematical works and a guardian of the temple, Thabit ibn Qurra proposed, in a short opuscule entitled "Correction of problems of algebra by geometric proofs," the first proofs "acceptable" to the community of geometers. The language and the type of reasoning are those of Euclid. The proof is divided into two parts. The objective of the first is to associate to the quadratic equation a geometric figure, while the second refers directly in its arguments to one of the propositions of Book II of the Elements. The logical forms "PàQ" and "Q because P" are very frequently used. Thabit proves the algorithm for equations whose coefficients are random numbers represented by segments, and not for particular cases. In this sense his proof has a more general and more intellectual character than that of al-Khwarizmi. He finishes each mathematical proof by showing the agreement between his results and those obtained by ahl al Jabr (the algebraists.) (Van der Waerden, pp. 18-20 or Berggren, pp 106-8.)
   While he cites as such the pragmatic proof of al-Khwarizmi, qualifying it as "visual", Abu Kamil, who is within the community of algebraists, presents a new geometric proof introduced by the term "the proof." He enriches the toolbox by including in it numerous algebraic identities proved geometrically in the manner of Euclid and based on his Elements. Describing Abu-Kamil's work, Sesiano states that "This need to justify algebraic reasoning in geometric mode, regarded as necessary by a branch that had not yet achieved autonomy, was pushed so far that one frequently finds in problems, in addition to the algebraic solution, a deduction of the formula on a figure." (Sesiano, p.71)
   The algebraist al-Karaji takes up the proofs of al-Khwarizmi and those of Abu Kamil. Systematizing their work and structuring its presentation, he begins with numerous introductory chapters which complete the algebraic toolbox by placing in it all the arithmetic propositions of whole numbers and of fractions and also those of quadratic irrationals, and by adding to it a maximum number of algebraic identities, all proved geometrically using Books II and VII to X of the Elements. Once the concept of unkown has been clarified, he finishes his work with the theory of equations and with a multitude of problems whose solution it makes possible.
   The major obstacle encountered in legitimizing the algebraic reasoning concerns the nature of the product of numbers, because while a number itself could be represented by a line segment, the product of two numbers by the area of a rectangle, and of three by the volume of a parallelepiped, the product of more than three numbers was no longer representable. "And if the algebraist uses the squared square [that is, the fourth power of a number] in problems of geometry" Omar al-Khayyam (1048-1131) tells us, "it is metaphorically, and not really, because it is not possible for a squared square to be a size." (R. Rashid - B. Vahabzadeh, p. 122.)
   Al-Karanji gets around this difficulty by creating the field of "known numbers" in parallel with the field of "unknown numbers". "Learn," says he, "that operating in the field of knowns keeps them in this field no matter what the operation." (Anbouba, p. 47). It is thus no longer a matter of reasoning on geometric figures but directly on numbers, which may themselves be the result of several operations on numbers. The toolbox of algebra thus integrates all the simple, but also the extremely complex, techniques of numerical arithmetic, in particular that laid out by Diophantos, and begins to liberate itself from the restrictions of geometry.

A geometric theory of equations

Since antiquity, numerous problems of geometry (such as that of trisecting the angle or that of the two means) lead to certain third degree equations. Omar al-Khayyam, collecting scattered results, attempted to classify all third degree equations and solve them. The resulting typology permits the identification of "all types of third degree equations, classified according to the distribution of constants and first, second and third degree terms, between the two members of the equation. For each of the types, al-Khayyam finds a construction of a positive root by the intersection of two conics" (R. Rashid, p.43) Omar al-Khayyam situates himself entirely within a Euclidean framework, by specifying the concepts of size and the units of measure used and by respecting the principles of homogeneity of the spaces on which one operates. He refers continually to the geometric and arithmetic chapters in the Elements, as well as to Appolonius's results on the properties of conics. For al-Khayyam, "numerical mathematical proof is conceived of when one conceives of geometric mathematical proof." (R. 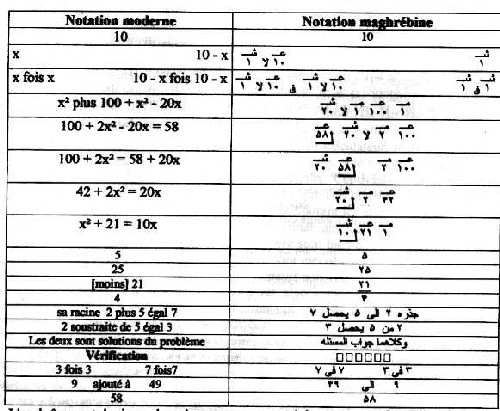Rashid- B. Vahabzadeh, p. 140.)
   The geometrical theory of equations attained its apogee with Sharaf ad-Din at-Tusi (1135-1213), who not only took back up the work of al-Khayyam, but deepened its mathematical proofs by placing himself at the intersection of Euclidean solid geometry and the geometry of conics, of which he proved the most useful properties. His mathematical proofs are general, the coefficients of the equations being random numbers. He demonstrates how to manipulate the types of object so as to make the results homogeneous: thus for example in the equation x = q, q is a segment of length q, while in x³ = q, the number q represents q times the volume of a unit cube. The metric properties of rectangles and parallelepipeds are implicit, although those of conics are invoked explicitly. The existence of positive solutions results most often from verification of the conditions for existence, which Sharaf ad-Din at-Tusi demonstrates by means of original and extremely elaborate geometric reasoning, based simultaneously on the reading of a diagram and a succession of syllogisms. He completes each geometric solution with a numeric solution inspired by Indian techniques of determining (on a dust table) square and cube roots of a whole natural number, but he does not content himself with exercising the algorithm on a numerical case assumed to be generic and instead gives a geometric justification for each step of the calculation.
The geometric theory of equations attained with Omar al-Khayyam and Sharaf ad-Din at-Tusi a level of complexity in its methods, its reasoning and its results such that it was never surpassed by the Arab mathematicians who followed them.

4. An arithmetic of polynomial expressions

From naïve proofs...

When al-Khwarizmi attempted to justify the sum of two trinomials, which we will denote in modern symbols: 100 + x² + -2x and 50 + 10x - x² , he noted his incapacity to represent this sum by a geometric figure. He wrote: "Since we cannot demonstrate it by a diagram, its necessity is thus linguistic." He thus proceeded as with the current practice which permits operation on sizes of the same nature (add numbers to numbers, roots to roots or squares to squares.) A naïve arithmetic of algebraic expressions was born, its principal reference being the arithmetic of whole numbers and of fractions. With Abu Kamil, then al-Karaji, this arithmetic was to develop into an autonomous science.

...to accepted algebraic proofs

Representation by tables

Self-proclaimed disciple of al-Karaji, As-Samaw'al (1130-1174) designated polynomials as being expressions with known images. In fact, the known images of which he speaks are the coefficients of the polynomials. He writes them in Arabic-Indian decimal notation and represents them in a table, the actual computations being carried out on a dust board. Thus, for example, " Three Kaâb plus two Mal, minus seven Shay, fourteen Dirham and thirty-seven parts of Mal ", i.e., in modern notation 3x³ + 2x² - 7x + 14 + 37x^-2, would be represented as follows:

The first line of the table contains the name of the powers (al-Maratib) of the unknown or their inverses. The second line contains the "known images", i.e., the coefficients written in Indian numbers. With the exception of one of the two extreme terms (that of highest or lowest degree) the other coefficients may be negative, the absence of a power being marked by a zero.
All of the algorithms of Arabic-Indian arithmetic can thus be generalized by analogy to the arithmetic of polynomials.

Maghrebian symbolic representation

While in the Orient the analogy between decimal notation of whole numbers and of expressions with known images resulted in the use of the dust board and of tables, this analogy led in Maghreb to the development of a symbolic notation for polynomial expressions, as is illustrated by the following hesitant representation of 8x⁹ + 48x⁸ + 132x⁷ + 208x⁶ + 198x⁵ + 108x⁴ + 207x³.

Conclusion

We have just recalled in a rapid and schematic manner the status of proof in Arabic algebra, attempting as we did so to stress the connectedness of the systems of knowledge in question: the practices of calculation in the IXth century, arithmetic and Euclidean geometry, decimal calculations and Indian numerical analysis, Diophantine methods of numerical analysis, all mastered better and better by the Arabian algebraists who thus constructed an autonomous science whose concepts and forms of reasoning evolved from an initial state of mumbling to a state of self-confidence, one which even permitted the use of a certain type of algebraic symbolism. The studies cited below in the bibliography make it possible better to discern these transformations and grasp their complexity.

Bibliography

Ahmad Salah et Rashed Roshdi (1972), Al-Bahir en algèbre d'as-Samaw'al, édition de l'Université de Damas.
Anbouba Adel (1964), L'algèbre al-Badii d'al-Karaji, Introduction en français, Publications de l'Université libanaise, Beyrouth.
Berggren J.L. (1986), Episodes in the Mathematics of Medieval Islam, Spinger-Verlag, New York.
R.Rashed-B.Vahabzadeh (1999), al-Khayyam mathématicien, Librairie Albert Blanchard, Paris.
Rashed Roshdi (1997), (sous la direction de) Histoire des sciences arabes, Tome 2: Mathématiques et physique, Seuil, Paris.
Sesiano Jacques (1999), Une introduction à l'histoire de l'algèbre, Presses polytechniques et universitaires romandes, Lausanne.
Van der Waerden (1980), A History of Algebra, Springer-Verlag, New York.

Reactions? Remarks?

The reactions to the contribution of Mahdi Abdeljahouad will be
published in the Spring 2002 Proof Newsletter

© Mahdi Abdeljahouad

  Translation Virginia Warfield

Back to the Newsletter