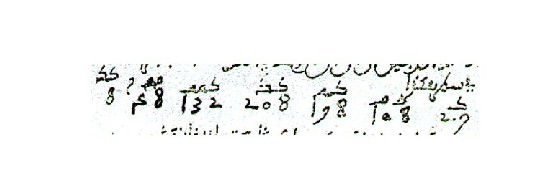|
La lettre de la Preuve |
|
ISSN 1292-8763 |
|
|
||
|
|
La preuve dans l'algèbre arabeMahdi Abdeljaouad
L'algèbre arabe s'est développée, à partir du IXe siècle en construisant une science issue des pratiques de calcul partagées par les différents acteurs de la vie quotidienne (artisans, commerçants, jurisconsultes, scribes, calculateurs, astronomes, …). Elle s'est structurée en trois systèmes de connaissances : les équations, les irrationnels et les inconnues. Ces systèmes, dont les prémisses se trouvaient déjà dans les sciences antiques et dans la science indienne, se sont édifiées à la fois selon leur propre logique et leurs propres méthodes, mais aussi sous l'intense influence des autres systèmes, constituant à partir du douzième siècle un corpus autonome avec ses spécialistes Ahl al-Jabr (les algébristes), ses concepts, ses types de raisonnements, ses stéréotypes et bien entendu ses résultats . Rechercher le statut de la preuve dans l'algèbre arabe nous oblige donc à identifier les types de preuves spécifiques à chaque système et en particulier ceux que les algébristes reconnaissent comme valides. 1. Une typologie des équations et leurs algorithmes associés Lorsque le calife al-Ma'moun demanda à al-Kwarizmi (780-650)
de rédiger le premier traité d'algèbre arabe, il
voulait mettre à la disposition des utilisateurs un outil synthétisant
les connaissances éparses concernant la résolution des
problèmes de la vie courante. L'opuscule d'al-Khwarizmi est très
court, son objectif annoncé est de codifier une pratique partagée
par les calculateurs : la mise en équation des problèmes
et la résolution des équations linéaires et quadratiques
à coefficients entiers ou fractionnaires positifs. Il identifie
six équations canoniques auxquelles, en principe, tout problème
doit se ramener et propose un algorithme pour la résolution de
chacune d'entre elles. L'originalité de ce travail ne se trouve
pas dans les algorithmes eux-mêmes, dont on retrouve certains
chez les Egyptiens, d'autres chez les Babyloniens et la plupart chez
les Indiens, mais dans la volonté de l'auteur de classer les
équations canoniques et de fixer un vocabulaire à la fois
pour les objets mathématiques : mãl (un bien),
jidhr (une racine) et ('adãd) (un nombre donné),
pour les relations et même pour les raisonnements. Ce vocabulaire
est familier à tout lecteur capable de calculer avec des entiers
naturels ou des fractions, les opérations : addition, soustraction,
multiplication, division et extraction de la racine carrée, se
pratiquent communément en arithmétique.
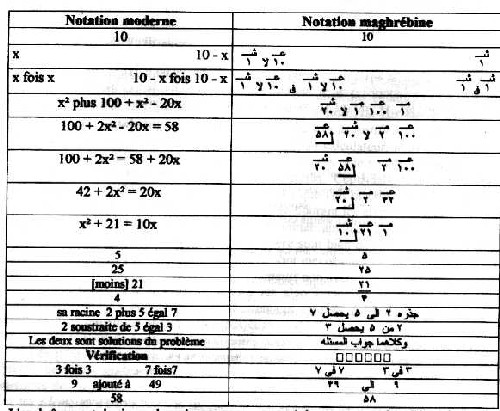
Ainsi dans l'exemple suivant : Un Mal et vingt et un égalent dix Jidhr, que l'on traduirait en notation moderne par x2 + 21 = 10x , dix est le nombre de Jidhr et vingt et un sont les 'Adad. L'algorithme revient à prendre la moitié de dix, c'est-à-dire 5, qu'on multiplie par lui-même; on obtient 25 dont on soustrait la constante 21 et on trouve 4. Sa racine carrée 2 est alors soustraite de 5 (moitié du coefficient de x); on trouve 2, première racine de l'équation donnée. Si la racine carrée 2 est ajoutée à 5, on trouve 7, deuxième racine de l'équation. Ces exemples génériques se retrouveront dans les traités
d'algèbre de la plupart des successeurs d'al-Khwarizmi.
La typologie des équations quadratiques sera étendue aux équations de degré trois par Omar al-Khayyam (1048-1131) et par Sharaf ad-Din at-Tusi (1135-1213) qui ne parvenant pas à leur proposer de solutions par radicaux leur chercheront des solutions géométriques. Nous évoquerons leur approche au paragraphe 3. 2. L'arithmétique des nombres irrationnels Alors qu'al-Khwarizmi n'utilisait que des entiers naturels et des fractions
comme coefficients des équations canoniques traitées.
Ses successeurs immédiats, comme Abu Kamil (850-930) ou plus
tardifs comme al-Karaji (953-1028), vont étendre les calculs
algébriques aux équations dont les coefficients peuvent
être irrationnels. L'arithmétique des irrationnels, qui
était embryonnaire chez al-Khwarizmi, devient un chapitre autonome
préliminaire à toute théorie des équations.
La boite à outils est explicitement euclidienne, comprenant le
chapitre X des Eléments d'Euclide, les raisonnements et
les vérifications étant géométriques. 3. Les preuves géométriques Ce qui distingue al-Khwarizmi de ses prédécesseurs de
l'Antiquité ou de l'Inde, c'est son soucis de justifier les algorithmes
de résolution des équations quadratiques. "J'ai
décris, écrit-il, les algorithmes exacts de résolution
[de ces équations] et j'ai établi, pour chacun un diagramme
qui permet de déduire la justification [du résultat]".
Cette partie du traité d'al-Khwarizmi ne sert à rien au
calculateur, mais elle permet de montrer que ce travail est scientifique,
en ce sens que ses objets mathématiques ont été
définis et les propriétés qui en découlent
démontrées. Cependant, ces preuves sont pragmatiques,
elles s'appuient sur des diagrammes que l'on place sous les yeux et
que l'on suit pas à pas en décrivant à l'aide du
langage courant les étapes du raisonnement : Ajout ou soustraction
de figures au diagramme initial, application des aires ou respect de
l'homogénéité des termes sur lesquels on opère
sont bien des pratiques euclidiennes (cf Arsac, 1999), mais les références
à Euclide sont inexistantes et son influence directe non avérée. Les preuves euclidiennes Spécialiste des œuvres mathématiques
grecques et gardien du Temple, Thabit ibn Qurra propose, dans un court
opuscule intitulé "Correction des problèmes d'algèbre
par des preuves géométriques", les premières
preuves "acceptables" pour la communauté des géomètres.
La langue et le type de raisonnements sont ceux d'Euclide. La preuve
est partagée en deux parties, la première a pour but d'associer
à l'équation quadratique une figure géométrique,
la seconde fait un appel direct dans les arguments à l'une des
propositions du Livre II des Eléments. Les formes logiques
'P à Q' et 'Q car P' sont très souvent utilisées.
Thabit prouve l'algorithme pour des équations dont les coefficients
sont des nombres quelconques représentés par des segments
et non sur des cas particuliers, en ce sens sa démonstration
possède un caractère plus général et plus
intellectuel que celle d'al-Khwarizmi. Il termine chaque démonstration
en montrant la concordance de ses résultats avec ceux obtenus
par ahl al Jabr (les algébristes). (Van der Waerden, pp.18-20
ou Berggren, p.106-8). Une théorie géométrique
des équations Depuis l'Antiquité, de nombreux problèmes
de géométrie (tels celui de la trisection de l'angle ou
celui des deux moyennes) se ramènent à certaines équations
du troisième degré. Omar al-Khayyam, ramassant les résultats
épars, a cherché à classer toutes les équations
de degré trois et à les résoudre. La typologie
obtenue permet d'identifier "tous les types d'équations
du 3e degré, classées de façon formelle selon la
répartition des termes constants, du premier degré, du
second et du troisième degré, entre les deux membres de
l'équation. Pour chacun des types, al-Khayyam trouve une construction
d'une racine positive par l'intersection de deux coniques"
(R.Rashed, p.43). Omar al-Khayyam lui-même se situe complètement
dans un cadre euclidien, en précisant les concepts de grandeur
et d'unité de mesure utilisés et en respectant les principes
d'homogénéité des espèces sur lesquelles
on opère. Il se réfère continuellement aux chapitres
géométriques et arithmétiques contenus dans les
Eléments, ainsi qu'aux résultats d'Apollonius pour
les propriétés des coniques. Pour al-Khayyam, "la
démonstration numérique se conçoit lorsqu'on conçoit
la démonstration géométrique" (R.Rashed-B.Vahabzadeh,
p.140). 4. Une arithmétique des expressions polynomiales Des preuves naïves … Lorsque al-Khwarizmi s'essaye à justifier la somme des deux trinômes, que nous noterions en symboles modernes : 100 + x2 + - 2x et 50 + 10x - x2 , il constate son incapacité à représenter cette somme par une figure géométrique. Il écrit : "Ne pouvant la montrer par un diagramme, sa nécessité est donc langagière". Il va donc procéder comme dans la pratique courante qui permet d'opérer sur des grandeurs de même nature (ajouter des nombres aux nombres, des racines aux racines ou des carrés aux carrés). Une arithmétique naïve des expressions algébriques est née, son référant principal étant l'arithmétique des entiers naturels et des fractions. Avec Abu Kamil, puis al-Karaji, cette arithmétique va se constituer en science autonome. … aux preuves algébriques acceptées S'interrogeant sur le statut de l'algèbre et le comparant à
celui de la géométrie, al-Karaji écrit : "L'une
se fonde sur la ligne et l'autre sur la chose [Shay] …Celle-là
possède une figure perçue par la vision, alors que celle-ci
possède une forme connue de manière innée, conçue
par l'esprit ... La chose, pour cette définition, est comme la
ligne que le géomètre rend connue pour pouvoir s'en servir
comme mesure et ainsi toutes les lignes qui lui sont commensurables
sont connues …" (S.Ahmad, p.72). Reprenant presque mot
pour mot le prologue de l'Arithmetica de Diophante, traduit en
arabe par Qusta ibn Luqa (870-912), al-Karaji fixe définitivement
la terminologie algébrique arabe : al-Majhoulãt
(les inconnus), ont composés de Shay (la chose), de ses
puissances successives (mãl , kaãb, mãl-mãl,
mãl-kaãb, etc) et de leurs inverses. On y opère
formellement en multipliant et divisant les inconnus entre eux, mais
aussi en ajoutant ou soustrayant les uns aux autres et en extrayant
leurs racines carrées, ce qui permet de définir de nouveaux
inconnus (qui ne sont autres que les expressions polynomiales : monômes,
binômes, trinômes, etc). al-Karaji précise : "…de
même, [opérer] dans le champ des inconnus permet
de les garder dans ce champ; cela veut dire qu'il restent toujours inconnus
tant qu'ils ne figurent pas dans une équation" (Anbouba,
p.47). Disciple auto-proclamé d'al-Karaji, l'algébriste As-Samaw'al (1130-1174), désigne les polynômes comme étant les expressions aux images connues . En fait, les images connues dont il parle sont les coefficients des polynômes, il les écrit en numération décimale arabo-indienne et les représente dans un tableau, les calculs effectifs se faisant sur une planche à poussière. Ainsi, par exemple, " Trois Kaâb plus deux Mal, moins sept Shay, quatorze Dirham et trente-sept parties de Mal " , c'est-à-dire en symboles modernes 3x3 + 2x2 - 7x + 14 + 37x-2 , sera représentée ainsi :
La première ligne du tableau contient le nom des puissances
(al-Maratib) de l'inconnu ou de leurs inverses. La deuxième
ligne contient les " images connues ", c'est-à-dire
les coefficients écrits en chiffres indiens. A l'exception d'un
des deux termes extrêmes (celui de plus haut degré ou celui
de plus bas degré), les autres coefficients peuvent être
négatifs, l'absence d'une puissance étant marquée
par le zéro. La représentation symbolique maghrébine Alors qu'en Orient, l'analogie entre l'écriture décimale des nombres entiers et celles des expressions aux images connues a entraîné l'utilisation de la planche à poussière et des tableaux, cette analogie favorisa au Maghreb le développement d'une écriture symbolique des expressions polynomiales, comme le montre la représentation hésitante suivante de 8x9 + 48x8 + 132x7 + 208x6 + 198x5 + 108x4 + 207x3 :
Nous venons d'évoquer d'une manière rapide et schématique le statut de la preuve dans l'algèbre arabe en essayant d'insister sur l'enchevêtrement des systèmes de connaissances en jeu : les pratiques de calcul du IXe siècle, l'arithmétique et la géométrie euclidiennes, le calcul décimal et l'analyse numérique indiens, les méthodes d'analyse numérique diophantiens, tous de mieux en mieux maîtrisés par les algébristes arabes qui construisent ainsi une science autonome dont les concepts et les raisonnements évoluent du stade du balbutiement initial au stade de la confiance en soi et qui , à son apogée, se permet même l'usage d'un certain type de symbolisme algébrique. Les études, citées ci-dessous dans la bibliographie, permettent de mieux cerner ces transformations et d'en saisir la complexité. Bibliographie Ahmad Salah et Rashed Roshdi (1972), Al-Bahir
en algèbre d'as-Samaw'al, édition de l'Université
de Damas.
Les réactions à la contribution de |
|