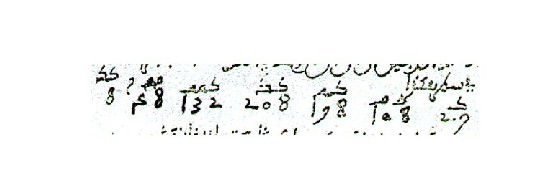La lettre de la Preuve

ISSN 1292-8763

   

La demostración en el álgebra de los árabes

El desarrollo del álgebra de los árabes comenzó en el siglo noveno como un intento de construir una ciencia basada en prácticas de cálculo que fueran comunes a varias ocupaciones (artesanos, comerciantes, jurisconsultos, escribas, calculadores, astrónomos, etc.). Esta ciencia se estructuró en tres sistemas de conocimientos : las ecuaciones, los irracionales, y las incógnitas. Estos sistemas, cuyas premisas se encontraban ya en las ciencias antiguas y en la ciencia india fueron construídos según su propia lógica y sus propios métodos, pero tambien bajo la intensa influencia de otros sistemas ; a partir del siglo XII esta disciplina había constituido un cuerpo autónomo de conocimientos, con sus propios especialistas Ahl al-Jabr (los algebristas), sus conceptos, sus tipos de razonamiento, sus estereotipos, y por supuesto sus resultados. Si intentamos entender el estatuto de la prueba en el álgebra árabe, nos vemos obligados a identificar los tipos de prueba específicos de cada uno de esos sistemas, y en particular aquellos que los algebristas reconocían como válidos.

1. Una tipología de las ecuaciones y sus algoritmos asociados

Cuando el califa al-Ma'moun pide a al-Kwarizmi (780-650) que éste escriba el primer tratado árabe del álgebra, su intención era poner a disposición del público una herramienta que sintetizara una multitud de conocimientos dispersos relativos a la resolución de problemas cotidianos. El tratado de al-Khwarizmi es breve, y su objetivo explícito es de dar un lenguaje para expresar una práctica comunmente usada por los calculadores : el uso de ecuaciones para representar problemas y la resolución de ecuaciones lineales y cuadráticas con coeficientes enteros o fraccionarios positivos. Al-Kwarizmi identifica seis ecuaciones canónicas a las que en principio todo problema debería poderse reducir ; y propone un algoritmo para la resolución de cada una de ellas. La originalidad de este trabajo no se encuentra en los algoritmos propiamente dichos, algunos de los cuales ya se encontraban en la matemática egipcia, otros en la de los babilonios y la mayoría en la matemática india. La originalidad se encuentra en la decisión del autor de clasificar las ecuaciones canónicas y de establecer un vocabulario tanto para los objetos matemáticos (por ejemplo, mãl-algo--, jidhr-una raíz-y 'adãd-un número dado) como para las relaciones y aún para los razonamientos. Todo lector capaz de calcular con enteros naturales o fracciones conoce algo de este nuevo vocabulario : para las operaciones, Al-Kwarizmi usa los términos adición, sustracción, multiplicación, y división que ya se usaban comunmente en aritmética.
   Las propiedades de conmutatividad y distributividad se demuestran mediante analogías con aquellas propiedades que valen para los números enteros. En cuanto a la designación de los nuevos razonamientos, ésta utiliza las expresiones que aparecen en el título de la obra : Kitab al-Jabr wal-Muqabala. La primera al-Jabr (restauración) designa la operación de deshacerse de los términos negativos que aparecen en uno de los miembros de la ecuación. La segunda al-Muqabala (oposición) designa la operación de reducción de términos semejantes, o términos de igual grado.
El algoritmo de resolución de una ecuación canónica se deriva a partir de un ejemplo genérico de ecuación numérica con coeficientes simples y donde al menos una raíz es positiva y casi evidente. Se trata de una sucesión de instrucciones estereotipadas :

El encademaniento lógico del razonamiento se traduce en una sucesión de ecuaciones o de resultados intermedios, cada uno de los cuales ocupa un renglón y se lee de arriba hacia abajo sin utilizar conectores lógicos. Las reglas son implícitas pero visibles.

Las ecuaciones de tercer grado

La tipología de las ecuaciones cuadráticas será extendida a las ecuaciones de tercer grado por Omar al-Khayyam (1048-1131) y por Sharaf ad-Din at-Tusi (1135-1213) quienes en lugar de proponer soluciones mediante radicales buscarán soluciones geométricas. Comentaremos sobre sus contribuciones en la sección 3.

2. La aritmética de los números irracionales

Mientras que al-Khwarizmi no utiliza sino enteros naturales y fracciones como coeficientes de las ecuaciones canónicas tratadas, sus sucesores inmediatos, como Abu Kamil (850-930), o posteriores como al-Karaji (953-1028) extienden los cálculos algebraicos a ecuaciones cuyos coeficientes pueden ser irracionales. La aritmética de los irracionales, embrionaria en al-Khwarizmi, deviene un capítulo autónomo preliminar a toda teoría de ecuaciones. Las herramientas usadas son explicitamente Euclideanas y se encuentran en el libro X de los Elementos de Euclides. Los razonamientos y las verificaciones son geométricas.
   Deben distinguirse dos evoluciones, sin embargo. Por una parte, se observa la naturalización de los métodos de cálculo con radicales, dejando progresivamente de lado las justificaciones geométricas. Por otra parte, se observa la invención de los magrebíes de uno simbolismo similar al simbolismo algebraico pero específico para el tratamiento de los radicales. A partir de allí se puede razonar con los radicales de la misma manera como se razona con los números, aplicando propiedades de commutatividad y distributividad a los números irracionales.

3. Las pruebas geométricas

Lo que distingue a al-Khwarizmi de sus predecesores de la antigüedad o de la India es su deseo de justificar los algoritmos de resolución de las ecuaciones cuadráticas. " He indicado " dice él " los algoritmos precisos para la resolución [de esas ecuaciones] y he propuesto para cada uno de ellos un diagrama que permite deducir la justificación [del resultado]. " Esta parte del tratado de al-Khwarizmi no sirve de nada al calculador, pero permite al autor mostrar que su trabajo es científico, en el sentido de que sus objetos matemáticos han sido definidos y las propiedades que se derivan de aquellos han sido demostradas. Sin embargo las pruebas son pragmáticas, se apoyan en diagramas a los que hay que observar y usar en un razonamiento cuyas etapas son asistidas por el lenguaje ordinario : Adición o sustracción de figuras al diagrama inicial, aplicación de areas o atención a la homogeneidad de los términos sobre los que se opera son practicas euclideanas reconocidas (cf Arsac, 1999) pero no se observan referencias directas a Euclides.
   Notemos además que al-Khwarizmi justifica los algoritmos de resolución de ecuaciones cuadráticas cuyos coeficientes son enteros naturales particulares. Estas ecuaciones son consideradas ejemplos genéricos y son retomadas por la mayor parte de los sucesores de al-Kwarizmi, aun aquellos que adoptan pruebas nuevas.
Las pruebas pragmáticas presentadas por al-Khwarizmi y basadas en una lectura directa de los diagramas no satisfacen ni a la comunidad de geómetras ni a la incipiente comunidad de algebristas ; los primeros consideraban que todo razonamiento debería de apoyarse explicitamente en los Elementos de Euclides y los segundos preferirían deshacerse de esa autoridad. Thabit ibn Qurra (826-900) es un integrante del primer grupo, mientras que Al-Karaji si bien prosigue sistemáticamente esa orientación [euclideana], tambien crea las condiciones para que se cuestione la tutela euclideana y por ello podría considerárselo como el verdadero inventor del álgebra como ciencia establecida, con su terminología, sus definiciones, sus proposiciones identificadas, y sus pruebas originales.

Las pruebas euclidianas

Como especialista en las obras matemáticas griegas y guardián del Templo, Thabit ibn Qurra propone, en un breve opúsculo intitulado " Corrección de problemas de álgebra mediante pruebas geométricas, " las primeras pruebas " aceptables " para la comunidad de geometras. El lenguaje y el tipo de razonamiento son los de Euclides. La prueba se divide en dos partes, la primera tiene como objetivo asociar a la ecuación cuadrática dada una figura geométrica, la segunda hace referencia directa en sus argumentos a las proposiciones del Libro II de los Elementos. Las formas lógicas " P implica Q " y " Q se sigue de P " se utilizan frecuentemente. Thabit prueba el algoritmo para las ecuaciones cuyos coeficientes son números cualesquiera representados por segmentos y no solo para casos particulares. En este sentido sus demostraciones poseen un caracter más general y más intelectual que aquellas de al-Khwarizmi. Thabit termina cada demostración mostrando la concordancia entre sus resultados y aquellos obtenidos por ahl al Jabr (los algebristas). (Van der Waerden, pp.18-20 ; Berggren, p.106-8).
   Luego de citar textualmente la prueba pragmática de al-Khwarizmi calificándola de "visual", Abu Kamil, un miembro de la comunidad de los algebristas, presenta una nueva demostración geométrica a la que introduce como " la prueba ." Abu Kamil enriquece la caja de herramientas mediante incluir una cantidad de identidades algebraicas demostradas geométricamente a la manera de Euclides y a partir de los Elementos. Refiriéndose al trabajo de Abu Kamil, Sesiano indica que " Esta necesidad de justificación more geometrico del razonamiento algebraico, vista como necesaria por una rama de la disciplina que no había ganado aun su autonomía, es tan evidente que uno la encuentra con frecuencia en los problemas, ademas de su resolución algebraica, una deducción de la formula a partir de una figura " (Sesiano, p. 71).
   El algebrista al-Karaji retoma las pruebas de al-Khwarizmi y de Abu Kamil. Sistematizando el trabajo de aquellos y estructurando su presentación, al-Karaji comienza con varios capítulos introductorios donde el completa el herramental algebraico, incluyendo todas las proposiciones sobre la aritmética de los enteros naturales y de las fracciones así como las de los irracionales cuadráticos y agregando una gran cantidad de identidades algebraicas, todas demostradas geométricamente a partir de los Libros II y VII a X de los Elementos. Una vez explicado con precisión el concepto de incógnita, al-Karaji termina su obra con una teoría de ecuaciones y una multitud de problemas que esta teoría permite resolver.
   El mayor obstáculo encontrado en la legitimación de los razonamientos algebraicos concierne la naturaleza del producto de números : en efecto, si bien un número por sí solo podría representarse mediante un segmento de recta, el producto de dos números mediante el área de un rectángulo, y el de tres números por el volúmen de un paralelepípedo, el producto de más de tres números no es representable. " Y si el algebrista emplea el cuadrado de un cuadrado [es decir la cuarta potencia de un número] en un problema de geometría, " dice Omar al-Khayyam (1048-1131), " esto es una metáfora, pues es imposible pensar el cuadrado de un cuadrado como una magnitud " (R.Rashed-B.Vahabzadeh, p.122).
   Al-Karaji da cuenta de aquella dificultad mediante crear un cuerpo de " números conocidos " en paralelo al cuerpo de " números desconocidos. " " Téngase en cuenta " dice " que operar dentro del campo de los conocidos los mantiene dentro de tal campo, sin importar cual sea la operación " (Anbouba, p.47). No se trata más, entonces, de razonar acerca de figuras geométricas sino directamente acerca de números, los cuales pueden resultar de varias operaciones sucesivas sobre números. Las herramientas del álgebra incluyen ahora todas las técnicas simples así como algunas extremadamente complejas de la aritmética numérica, en particular aquellas técnicas elaborads por Diofanto. Así el álgebra empieza a liberarse de la tutela de la geometría.

Una teoría geométrica de las ecuaciones

Desde la antigüedad, numerosos problemas de geometría (tales como el de la trisección del ángulo o el problema de las dos medias) se reducen a ciertas ecuaciones de tercer grado. Omar al-Khayyam, organizando resultados dispersos busca clasificar todas las ecuaciones de tercer grado y resolverlas. La tipología obtenida permite identificar " todos los tipos de ecuaciones de tercer grado, clasificadas formalmente según donde se ubican en los miembros de la ecuación, los términos constantes, los de primer grado, los de segundo, y los de tercer grado. Para cada uno de esos tipos, al-Khayyam encuentra una construcción de una raíz positiva para la intersección de dos cónicas " (R.Rashed, p.43). Omar al-Khayyam tambien se sitúa completamente dentro del marco teórico euclideano, haciendo precisos los conceptos de magnitud y unidad de medida utilizados y respetando los principios de homogeneidad en las especies con las que él opera. Omar se refiere contínuamente a los capítulos geométricos y aritméticos contenidos en los Elementos, así como a los resultados de Apolonio sobre las propiedades de las cónicas. Para al-Khayyam, " la demostración numérica se concibe a partir de la concepción de la demostración geométrica " (R.Rashed-B.Vahabzadeh, p.140).
   La teoría geométrica de las ecuaciones alcanza su apogeo con Sharaf ad-Din at-Tusi (1135-1213), quien no solamente retoma los trabajos de Omar al-Khayyam sino tambien profundiza las demostraciones, ubicandose en la intersección de la geometría euclideana de sólidos y la geometría de las cónicas-de las cuales prueba las proposiciones más útiles. Sus demostraciones son generales, los coeficientes de las ecuaciones son arbitrarios. Sharaf muestra como manipular las cantidades para que el resultado sea homogéneo : así por ejemplo, en la ecuación x = q , q es un segmento de longitud q, mientras que en x³ = q , el número q representa q veces el volumen de un cubo unitario. Las propiedades métricas de los rectángulos y paralelogramos quedan implícitas, mentras que las de las cónicas se evocan explícitamente. La existencia de soluciones positivas son a menudo tributarias de la verificación de las condiciones de existencia que Sharaf ad-Din at-Tusi demuestra mediante razonamientos geométricos originales y extremadamente elaborados basados a la vez en la lectura de un diagrama y en una cadena de silogismos. Sharaf completa cada solución geométrica mediante una solución numérica inspirándose en técnicas indias de determinación (en una pizarra) de raíces cuadradas y cúbicas de un entero natural. Pero no se contenta con exponer el algoritmo usando un ejemplo numérico, él tambien justifica geométricamente cada paso del cálculo.
La teoréa geométrica de las ecuaciones obtiene con Omar al-Khayyam y Sharaf ad-Din at-Tusi tal nivel de complejidad, en sus métodos, sus razonamientos y sus resultados, que no será superada por les matemáticos árabes posteriores.

4. Una aritmética de las expresiones polinomiales

De las pruebas ingenuas …

Cuando al-Khwarizmi se esfuerza por justificar la suma de dos trinomios, a los que nosotros escribiríamos como 100 + x² + - 2x et 50 + 10x - x² él nos demuestra su incapacidad para representar tal suma mediante una figura geométrica. Dice " No pudiendo mostrarla mediante un diagrama, su necesidad sigue del lenguaje. " Y procede según la práctica ordinaria de operar sobre cantidades comparables (sumar números a los números, raices a las raices, cuadrados a los cuadrados). Una aritmética ingenua de las expresiones algebraicas surge, teniendo como principal referente a la aritmética de los enteros naturales y de las fracciones. Con Abu Kamil, y luego con al-Karaji, esta aritmética se constituirá luefgo en ciencia autónoma.

… a las pruebas algebraicas aceptadas

Preguntándose acerca del estatuto del algebra y comparándolo al de la geometría, al-Karaji escribe : " La una se funda sobre el segmento, la otra sobre la cosa [Shay]… La primera posee una figure percibida por la visión, mientras que la segunda posee una forma conocida de manera innata, concebida por la inteligencia… La cosa, de acuerdo con esta definicion, es como el segmento a la cual la geometría descubre para poder usarlas como medida, y así todos los segmentos que son conmensurables son conocidos… " (S.Ahmad, p.72). Retomando casi palabra por palabra el prólogo de la Aritmética de Diofanto, traducida al árabe por Qusta ibn Luqa (870-912), al-Karaji fija definitivamente la terminología algebraica árabe : al-Majhoulãt (las incógnitas), se componen de Shay (la cosa), de sus potencias sucesivas (mãl , kaãb, mãl-mãl, mãl-kaãb, etc) y de sus inversas. Se opera con ellas formalmente, multiplicando y dividiendo las incógnitas entre ellas, y tambien sumando o restando los unos a los otros y extrayendo raíces cuadradas, lo que permite definir nuevas incógnitas (que no son otras que las expresiones polinomiales : monomios, binomios, trinomios, etc. ). Al Karaji precisa : " igualmente, [operar] en el campo de las incógnitas permite mantenerlas dentro de ese campo ; es decir que se mantienen siendo incógnitas a menos que sean parte de una ecuación " (Anbouba, p.47).
   En este campo, casi todos los enunciados habían sido verificados geométricamente de antemano, pueden emplearse sin necesidad de reconsiderar su validez. Al-Karaji introduce esta manera de proceder mediante la expresión : " se prueba a la manera de Diofanto. "

La representación mediante tablas

Un autoproclamado discípulo de al-Karaji, el algebrista As-Samaw'al (1130-1174), designa a los polinomios como las expresiones con imágenes conocidas. En efecto, las imágenes conocidas de las que él habla son los coeficientes de los polinomios, a los que él escribe usando la numeración decimal indoárabe y los representa usando una tabla, haciendo los cálculos en una pizarra. Así, por ejemplo, " Tres Kaâb más dos Mal, menos siete Shay, catorce Dirham y treinta y siete partes de Mal " lo que en símbolos modernos sería 3x³ + 2x² - 7x + 14 + 37x^-2 , él lo representa como:

La primera línea de la tabla contiene el nombre de las potencias (al-Maratib) de la incógnita o de sus inversos. La segunda línea contiene las " imágenes conocidas, " es decir los coeficientes escritos en cifras indias. Con la excepción de uno de los dos términos extremos (el de mayor o el de menor grado), los otros coeficientes pueden ser negativos, y la ausencia de una potencia se indica con un cero. Todos los algoritmos de la aritmética indoárabe se pueden generalizar por analogía para la aritmética de los polinomios.

La representación simbólica magrebí

Mientras que en Oriente la analogía entre la escritura decimal de los números enteros y aquella de las expresiones en imágenes comunes implica la utilización de la pizarra y de las tablas, esta analogía le permite al Magreb desarrollar una escritura simbólica de expresiones polinomiales como lo muestra la siguiente representación de (probablemente) 8x⁹ + 48x⁸ + 132x⁷ + 208x⁶ + 198x⁵ + 108x⁴ + 207x³ :

Conclusión

Hemos evocado de manera rápida y esquemática el estatuto de la prueba en el álgebra de los árabes, tratando de insistir sobre la dependencia mutua de los sistemas de conocimientos en juego : las prácticas de calculo del siglo IX, la aritmética y la geometría euclideanas, el cálculo decimal y el análisis numérico de los indios, los métodos diofantinos de análisis numérico, todos los cuales son cada vez más diestramente manejados por los algebristas árabes quienes así construyen una ciencia autónoma en la cual los conceptos y los razonamientos evolucionan desde el estadio del balbuceo inicial al estadio de la confianza en sí mismo y que, en su apogeo, se permite a sí mismo el uso de un cierto simbolismo algebraico. Los estudios citados en la bibliografía permiten entender mejor estas transformaciones y aprehender su complejidad.

Bibliografía

Ahmad Salah et Rashed Roshdi (1972), Al-Bahir en algèbre d'as-Samaw'al, édition de l'Université de Damas.
Anbouba Adel (1964), L'algèbre al-Badii d'al-Karaji, Introduction en français, Publications de l'Université libanaise, Beyrouth.
Berggren J.L. (1986), Episodes in the Mathematics of Medieval Islam, Spinger-Verlag, New York.
R.Rashed-B.Vahabzadeh (1999), al-Khayyam mathématicien, Librairie Albert Blanchard, Paris.
Rashed Roshdi (1997), (sous la direction de) Histoire des sciences arabes, Tome 2: Mathématiques et physique, Seuil, Paris.
Sesiano Jacques (1999), Une introduction à l'histoire de l'algèbre, Presses polytechniques et universitaires romandes, Lausanne.
Van der Waerden (1980), A History of Algebra, Springer-Verlag, New York.

Regreso a la gacetilla