Shortcuts in
Proof
by
Jean-Paul Delahaye
Universite des Sciences et Technologies de Lille
Some
illustrations...

4. Proofs without
words
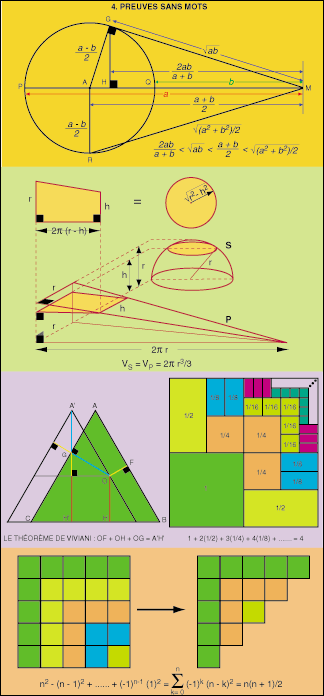

5. A heuristic
proof which cannot (today) be transformed into a formal
mathematical proof.
Consider the sequence of natural numbers defined as
follows:
x1 = 2
x2 = [the smallest prime factor of
x1 + 1] = 3
x3 = [the smallest prime factor of
x1 x2 + 1] = 7, … ,
xn+1 = [the smallest prime factor of
x1 x2 … xn+ 1]
, …
The sequence begins with 2, 3, 7, 43, 13, 53, 5, 6221671,
38709183810571, 139, 2801, 17, 5471, …This
Euclid-Mullin sequence lists only distinct primes: yn
= x1x2... xn + 1 is
not divisible by x1 (since if it were , then 1
would also be, as the difference of two numbers divisible by
x1.) The number yn is not divisible by
x2 (otherwise 1 would be), etc. Since yn is not
divisible by any of the prime numbers x1,
x2,...., xn, xn+1 is a new
prime number, and thus all of the xi are distinct prime
numbers. The question is knowing whether this sequence lists
all prime numbers, omitting none (though to be sure they
will be out of order.) It is thought that the answer is yes,
and the following heuristic proof is proposed:
Suppose the sequence did not include all of the
prime numbers. Let p be the smallest prime number not in
the sequence. Beyond a certain N, all prime numbers less
than p will be included in the numbers x1,
..., xN. If n is a randomly chosen whole
number larger than N, then the number yn =
x1x2... xn + 1 can be
considered a random number relative to p, and thus this
number has one chance in p of being a multiple of p
(since one out of every p whole numbers is a multiple of
p.) The number yn thus has probability (1 - 1/p) of not
being a multiple of p, which is also the probability that
xn+1 is different from p. The probability that
neither xN+1, nor
xN+2,…,xN+k is equal to p is
thus (1 - 1/p)k, which tends to 0 at infinity.
Otherwise stated, the probability that p does not appear
in the sequence xn is zero. Thus p appears in
the sequence, which contradicts its definition. Thus
every prime number p appears in the sequence
xn, which is the same as the list of prime
numbers, without repetition and written out of order.
Such a line of reasoning almost holds good, but it
assumes that yn is chosen at random, which is not
the case, and thus without a complement (which no one has
succeeded in discovering and which appears to be beyond the
range of current mathematics) the heuristic proof is not an
acceptable proof.

|