
© F.
Olivero
|
Theoretical background
In recent years some crucial aspects of mathematics have
been reduced in importance, or even removed from the basic
requirements of high school in some countries. Proof is one
of these. Diminishing the importance of some features of
mathematics in schools may compromise the quality of
students' intellectual development and may compromise the
specific role of cultural transmission that schooling plays
within the mechanism of cultural reproduction in a society
(Boero, 2000).
There is an ongoing debate within the
Mathematics Education research community tackling the
problem of the teaching and learning of proof from different
perspectives: historical, epistemological, cognitive and
didactical. Historical and epistemological studies on proof
have shown that proof is crucial in mathematics. This
suggests that, despite all the difficulties they have in
approaching proof, as identified in the literature, students
should be presented with this mathematical experience.
Cognitive and didactical studies may provide useful insights
into possible successful ways of introducing students to
proof. Many studies have focused on proof as a final product
providing different classifications of students' proofs
(e.g. Harel & Sowder, 1996). However processes of proof
production need to be investigated in order to find elements
which are fundamental to make the transition to proof
happen.
Italian researchers have developed a common
theoretical and analytical framework aimed at analysing
students' processes of production of 'theorems' (a unity of
statement, proof and reference theory), with focus on the
complex processes used when exploring, conjecturing and
constructing proofs in open problems within different
environments (paper & pencil, computers, mechanisms) and
different contexts (geometry, arithmetic, algebra). The
analytical tools which have been developed are: fields of
experience (Boero, 1992); semiotic mediation and semiotic
mediation within microworlds (Mariotti & Bartolini
Bussi, 1998; Bartolini Bussi & Mariotti, 1999);
Cognitive Unity (Boero et al, 1996; Mariotti et al,
1997).
Within this framework, the research group I
belong to in Turin has investigated in particular the role
of mediation of a dynamic geometry environment in the
proving process. A first teaching experiment was carried out
two years ago. The conclusion from that project was that
Cabri was a mediator in the transition to proof because of
the dragging function, which allows students to perform
experiments with geometrical figures, that otherwise might
be difficult because carried out only in the mind. Dragging
figures on the screen allows students to carry out
explorations which experts are more likely to do
spontaneously in the resolution of a problem. Different
dragging modalities used by students were identified and
their cognitive counterpart analysed. A model describing the
proving process was developed; it revealed that there was an
evolution in the use of the dragging modalities,
corresponding to a shift from conjectures to proofs
[*]
(Arzarello et al, 1998a, 1998b; 1999).
New classroom observations, both in Italy and in
England, have highlighted a much more complex situation
concerning the evolution of the dragging modalities and
shown the need for taking into account the whole learning
environment. For example, students do not use dragging
throughout the whole proving process when working in a
dynamic geometry environment, but there are moments in which
they need to stop dragging and work on the static Cabri
figure. Moreover it seems that students do not make use of
Cabri only, when provided with proving activities to be
tackled in that environment. Most of them still use paper
and pencil and/or other tools available to them in the
classroom. In particular we observed the use of sketches on
paper, especially after having produced a conjecture in
Cabri.
The project I am carrying out for my
PhD [*]
focuses on the analysis of the processes leading students to
the construction of a 'proven conjecture' (i.e. a
mathematical object "A(B") in geometry. Particular attention
will be paid to the role of mediation played by a dynamic
geometry environment (Cabri-Geometre) and its characterising
features and to the interaction with the other tools
(different forms of oral and written languages) which may
support students in that transition. Cabri is explicitly
introduced by the teacher in the classroom as a mediator, in
the sense that teachers use Cabri "to direct the learner in
the construction of meaning mathematically consistent"
(Mariotti, 2000), i.e. in order to support students towards
the construction of proofs. Students use Cabri as a tool in
order to solve the problems they are given, and in this
sense it functions as a semiotic mediator, "i.e. meanings
may emerge from subjects involvement in the activity"
(Mariotti, 2000). Within Cabri, different elements can be
object of mediation: dragging, constructions, measures,
etc…. The elaborated framework will show which elements
are fundamental to make this transition happen. Therefore it
will show how certain ways of approaching proof may be
successful in the classroom, and consequently it will
provide the basis for a teaching experiment to be
implemented and evaluated afterwards.
This contribution will illustrate a preliminary
analysis of students' protocols which introduce relevant
elements to be further investigated, with particular respect
to the analysis of the links between the genesis of
conjectures and the genesis of proofs within the proving
process, in terms of processes of reasoning, forms of
representations (language, metaphors, dragging, …),
physical referents (gestures, …) and theory. Taking on
board the embodied cognition perspective, one of the aims is
to analyse how a typically conceptual (and theory-based)
activity like proving may be rooted in "perceptual,
motor-program, emotional, historical, social and linguistic
experience" (Johnson, 1987). This is analysed according to
the construct of semiotic mediation.
A preliminary analysis
The following examples are taken from a protocol of a
pair of students (17 years old) solving an open problem
within Cabri (but similar observations were made in
protocols from other classrooms).
|
The problem is the "Angle bisectors problem"
(fig.1):
Let ABCD be a quadrilateral. Consider the
bisectors of its internal angles and the
intersection points H, K, L, M of pairs of
consecutive bisectors.
1. Drag ABCD, considering different
configurations. What happens to the
quadrilateral HKLM? What kind of figure does it
become?
2. Can HKLM become any quadrilateral?
3. Can HKLM become a point? Which hypothesis on
ABCD do you need in order to have this
situation?
|
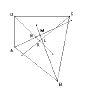
Figure 1
|
The problem was used as part of a classroom experience
[*] carried
out with six Further Maths A-level students (17 years old)
aimed at introducing students to processes of proving,
exploiting the potentialities of open problems and of the
Cabri environment. The project consisted of: 7
classroom-based sessions, aimed at introducing the basic and
essential ideas involved in the process of proving
statements in mathematics, moving from the elaboration of
conjectures to their justification and formalisation and a
project work. The classroom-based sessions involved three
phases. First, the teacher introduced the problem. Second,
students solved the problem in groups with Cabri and paper
& pencil, so producing conjectures & proofs. Third,
the teacher orchestrated a general discussion, in which
students exposed, confronted and discussed their conjectures
and proofs, co-ordinated by the teacher.
In each session we video recorded one pair of
students while solving the problem and the final
discussion.
In the following I will outline some of the
relevant elements of analysis which will ultimately be
elaborated in a more comprehensive model describing and
interpreting the whole proving process.
Generation of conjectures with the
mediation of dragging and language.
The following excerpt illustrates the mediation of the
dragging function in the generation of a conjecture. At the
same time, it can be observed the evolution of the language
students use over the generation process.
|
Students' work
Analysis
|
Analysis
|
|
The students are explaining to the teacher the
conjecture that if ABCD is a parallelogram then
HKLM is a parallelogram too, which they have
previously discovered.
127. A makes it (ABCD) to have a square inside
(HKLM) and it says 'object are parallel'.
128. A: yes?
129. T: ??
130. A uses check property for external
quadrilateral.
131. A: these two
are parallel…right OK.
132. A moves the side CD
133. W: they are
always parallel!
134. A: oh yes, they are always parallel!
135. T: because you are
moving a side now, that's OK.
136. A: yeah. So any
parallelogram
137. W: so whenever
the outside lines are parallel the inside ones
are.
138. While saying this A stops for a second.
|
In 131 'These two' refers to two particular
lines of a particular figure. It is an observation
of a property on the figure.
Dragging CD provokes a generalisation from the
particular observation to a general statement
saying the property is 'always' true (133).
After that, a justification in terms of dragging
within Cabri is given (135).
In 136 a 'translation' of dragging into geometry
occurs through language: dragging CD is
'translated' in the geometric statement 'any
parallelogram'. Moreover this last figure is no
more referred to as a particular parallelogram
('this'), but it represents a generic object ('any
parallelogram').
At the end (137) the conjecture is general and
it is formulated in a deductive form ('whenever
…'). The students have so validated their
conjecture while constructing it.
|
A and W are the students; T is the
teacher
Links between elements of the
conjecture which are the basis for the proof.
One of the main points of the Cognitive Unity framework
is the fact that students seem to 're-play' in the proving
phase the processes they used in the conjecturing phase and
to re-use the same elements but with a different function.
The following example shows how the element which made the
students produce the conjecture about the parallelogram, is
the central element around which the proof is
constructed.
|
Students' work
Analysis
|
Analysis
|
|
45. A: If those
lines (two sides) are
parallel then these are parallel (two
bisectors) (see Fig.2)
[….]
137. W: so whenever
the outside lines are parallel the inside ones
are.
[…]
At the end A wants to prove this conjecture.
She works on paper.
403. A: yes I'm trying to do the parallelogram.
If you know that…they are the same angles
right, because opposite angles are equal, those are
bisectors.
404. Silence. A uses a pen to redraw the
bisectors she has already drawn (Fig.3).
405. A draws the diagonal
406. W. Say that that angle…
407. A: well you can say; I know how you do it
right? If you draw the diagonal there right? (she
draws it) Then you know that that angle there, the
big one, is equal to that angle there (between the
sides and the diagonal).
408. W. Yes
409. A:. so that tiny bit equals that tiny
bit.
410. W: because that's equal to that
45. A:yeah. Therefore
those alternate angles are equal therefore those
two are parallel (the bisectors).
|
 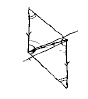
Figure
2 Figure
3
The conjecture A makes in 45 involves just a
part of the figure (the parallelism of the
bisectors). The language refers to 'those lines',
i.e. to a particular figure.
Line 137 represents a general conjecture (whose
generation has been explained above).
In 405 A draws the key element for the proof,
which then centres around showing that the
bisectors are parallel. This was the same element
leading her to formulate the conjecture.
It is interesting to notice that in the
construction of the proof the language uses again
'those', 'that', etc. However I would suggest that
this language has a different meaning from the same
words used in the conjecturing phase.
|
Oral and written
proofs.
In order to construct the product A(B the following
transitions are fundamental:
• from temporal narratives to mathematical
logic, via the generation of conditional statements;
• from actions to relationships;
• from perceptions to concepts;
• from descriptions to representations, via a
generalisation process.
"Theorems are out of time and out of history, it is like
they have lived for ever" (…), while our everyday
experience and the empirical practices in Cabri are embedded
in time. They follow a temporal logic, while a proof has to
follow a mathematical logic, based on the logical
consequences of statements. Students often provide
chronological accounts of actions carried out rather than
pointing out connections and implications. We can view proof
like a snapshot, while empirical practices can be
represented as a film. The fact that in a proof the
arguments need to be written in a deductive order needs
restructuring the actions which led students the proof
itself and reveals difficult.
It is interesting to see how this pair of students
generate the proof for their main conjecture
[*] : it
consists of a dynamic evolution from an oral proof on a
static Cabri figure to the explanation of the proof to the
teacher to an oral proof based on sketches on paper to a
written proof to be presented to the classroom. It seems
that when they change tool (oral/written language,
Cabri/paper&pencil), the students need to re-construct
the proof. In particular the passage from oral to written
proof is not just a matter of 'translating' a proof.
The oral proof in Cabri starts off in this way:
|
208. W: so you have one line going straight
through the middle obviously (the diagonal AC).
Then those two(the bisectors of <B and <D))
must meet in the middle again.
|
The organisation of the sketches in Figure 4 does not follow
a sequential logic. They started off that figure with the
intention of writing the final proof, but then while trying
to write they re-constructed it through the sketches .
Figure 5 is what the students considered to be a final
product. Not very much of the actual proof is present on
that paper.

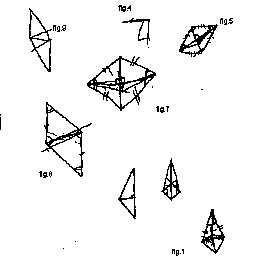
Figure
: sketches for the proof on paper. The
sketches are numbered in the order of
construction

Figure
: proof to be presented to the whole
classroom.
General structure of the protocol,
showing a similarity between the genesis of proofs and of
conjectures.
From this and other observations, it can be observed that
the whole proving process seems to develop according to a
dynamic evolution of the following phases, which are not
necessarily sequential. A similar structure between the
genetic process for conjectures and for proofs is
suggested.
1. Exploration in
Cabri. Figures are dragged and properties are discovered
(invariants, etc…). The students see things and
mainly describe what they see.
2. Oral formulation of a
conjecture/conjectures. It happens the conjectures are
produced simultaneously, many at the same time and quite
messy.
3. Writing the conjectures.
Now they are produced in a form "when…" or
"if…then" and more organised.
4. During the exploration
phase, elements of justification are already present and
mixed with the actual conjectures.
5. Constructing a proof,
working on paper sketches (or looking at the still Cabri
figure) and using gestures (hands, pens). It is still
very messy. A lot of statements are produced but not yet
ordered in a logical form.
6. Writing a proof. Even
when the students seem to agree on a proof, when they
have to write it down they re-work it because the fact
they have to 'translate' into a logical form, getting
read of the temporal sequence of events.
The actual sequence in the protocol of A and W is the
following.
1 - exploration
(1-202)
5 - constructing a proof for
the case of the kite (203-287) and explaining it to the
teacher (288-321)
3
- writing conjectures in the Cabri workspace
(322-
6-5-3 - A wants to write the
proof for the kite but they have to rework it again.
(340-398)
5 - A constructs the proof
for the parallelogram (399-412)
6 - A writes down the proof
on OHP (413-418)
Final remarks and
questions
From these excerpts some main elements to be investigated
emerge, which can be made explicit in the following research
questions.
• When and how do students start the
proving process, that is asking why a certain proposition
hold?
• What are the genetic processes in the construction
of proofs? Can a continuity be identified between the
genesis of conjectures and the genesis of proofs? What
elements provide this continuity?
• What is the mediating role of the dragging
function in the proving process? In particular, what
elements make it a support in the transition from
empirical to theoretical practices?
• What other Cabri elements mediate the proving
process? How?
• How do students integrate Cabri in their own
thinking processes?
• What is the evolution of students' use of
oral and written language over the process?
• What other forms of external representations
(e.g. sketches, drawings, etc…) are used in the
proving process? When and how?
References
Arzarello F., Olivero F., Paola D.,
Robutti O. (1999). Dalle congetture alle
dimostrazioni. Una possibile continuità cognitiva,
L'insegnamento della matematica e delle scienze integrate,
vol.22B, n.3.
Arzarello F., Micheletti C., Olivero
F., Paola D., Robutti O. (1998a) 'A model
for analysing the transition to formal proofs in geometry'.
In: A. Olivier & K. Newstead (eds.), Proceedings of
PME22, Stellenbosch, South Africa, vol. 2, pp. 24-31.
Arzarello F., Gallino G., Micheletti
C., Olivero F., Paola D., Robutti O.
(1998b) 'Dragging in Cabri and modalities of transition
from conjectures to proofs in geometry'. In: A. Olivier and
K. Newstead (eds.), Proceedings of PME22, Stellenbosch,
South Africa, vol. 2, pp.32-39.
Bartolini Bussi M. G., Mariotti M. A. (1999b)
'Semiotic mediation : from history to mathematics
classroom', For the Learning of Mathematics, 19 (2),
27-35.
Boero P. (1992) 'The crucial role of semantic fields
in the development of problem solving skills', in J. P.
Ponte et al. (eds), Mathematical Problem Solving and New
Information Technologies, Springer-Verlag, Berlin
Boero P., Garuti R., Mariotti M.A.
(1996) 'Some dynamic mental processes underlying producing
and proving conjectures', Proc. PME XX, Valencia, vol.
2,121-128.
Harel G., Sowder L. (1996) Classifying
processes of proving, Proceedings of PME XX, Valencia,
vol.3, 59-66.
Johnson M. (1987) The body in the mind: the bodily
basis of meaning, imagination and reason, Chicago: The Univ.
of Chicago Press.
Mariotti M.A., Bartolini Bussi M.G. (1998)
From drawing to construction: teacher's mediation within the
Cabri environment, Proceedings of PMEXXII, Stellenbosch,
vol. 3, 247 254.
Mariotti M.A., Bartolini Bussi M., Boero
P., Ferri F., Garuti R. (1997) Approaching
geometry theorems in contexts: from history and epistemology
to cognition, Proceedings of PMEXXI, Lathi, v.1,
180-195.
Notes
1. An account of the
study is provided in the quoted references.
[Back]
2. The project is carried out within a
collaboration between the University of Turin and the
University of Bristol. [Back]
3. This project was carried out by: G.
Moënne, C. Mogetta, F. Olivero & R. Sutherland,
Graduate School of Education, University of Bristol.
[Back]
4. The conjecture was first formulated in
this way: So for HKLM to be a point…when is that?
when it's two sides next to each other then must be equal.
That should work. [Back]
|







