
© Lulu
Healy
|
A consistent theme in research into proof in school
mathematics is the relationship between empirical evidence
and analytic argument. In general, this relationship has
been seen as a problematic one, with the vast majority of
students far from clear about the distinction between
inductive and deductive reasoning. Some researchers have
suggested that the cognitive gap between different modes of
reasoning parallels a profound epistemological gap between
ordinary argumentation (in which appeals to empirical
evidence are accepted and commonplace) and mathematical
proof (Balacheff, 1988; Duval, 1991). Rather than focussing
on discontinuities, a number of recent studies, on the other
hand, have stressed connections between different aspects of
the proving process. Examples include Simon's idea of
transformational reasoning (Simon, 1996), the cognitive
unity of statement, proof and theory proposed by Mariotti,
Bartolini Bussi, Boero, Ferri and Garuti (1997), and the
consideration of role of abductive reasoning in the
construction of proofs by Arzarello, Micheletti, Olivero and
Robutti (1998a).
This paper too concerns the building of
connections between different aspects of the proving
process. A number of examples of the kinds of the proof
constructions produced by English and Welsh students will be
presented in order to consider the ways in which they
co-ordinate (or not) empirical and theoretical modalities
and how this co-ordination is shaped by different approaches
to teaching proof.
First examples, then
explanations

Figure 1:
Explaining with reference to
structure
|
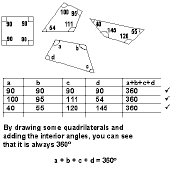
Figure 2:
Explaining with reference to action
|
Figure 1 presents an argument constructed to prove that
the sum of two odd numbers is always even, while the
argument in Figure 2 is an attempt to prove that the sum of
the interior angles of a quadrilateral is always 360º.
There are some similarities between the structure of these
two arguments, but also a rather important difference. Both
arguments contain a set of examples which confirm the
conjectured condionality and which is followed by a written
observation of why the given statement is true, but the
nature of the respective observations indicates
substantially different interpretation of what it means to
explain. In the first, the explanation focuses on the
mathematical properties underlying the examples, whereas the
second explanation involves a description of the actions
through which confirming evidence was produced.
Amongst the 2459 high-attaining mathematics
students (14-15 years old) who attempted to construct proofs
for these two statements, arguments with this structure
&endash; examples followed by observation &endash; were the
most common constructions produced. This is not all that
surprising since, in our mathematics curriculum students are
encouraged to approach proving in this way. Proof and
justification activities are located largely in activities
collectively known as "investigations" where data are to be
generated, synthesised into the articulation of a general
conjecture to be explained and, if possible, proved. As
suggested within the hierarchy of levels by which our
mathematics curriculum is organised (Department of
Education, 1995), the different aspects of the proving
process are interpreted as representative of ascending
levels of reasoning, with inductive processes associated
with lower levels than deductive ones. The result is that
the former are introduced before, and usually independently
from, the latter. A few students seem to be able traverse
the implied developmental passage from the empirical to the
theoretical for themselves and, when this happens (as can be
seen in Figure 1), the arguments produced are meaningful and
creative. In general, however, the generation of an
appropriate set of examples does not necessarily motivate in
students a need for deductive proof. We can say that there
seems to be no natural progression from empirical and
theoretical reasoning.
According to Duval (1998), any model of
mathematics learning in which different ways of reasoning
are organised according to a strict hierarchy is
inappropriate. Rather than being representative of higher
(or lower) levels of thinking, he argues that different
kinds of cognitive activity have their own specific and
independent development. This might suggest the structuring
activities to separately address specific types of thinking
processes. Instead, we chose to develop computer-based
situations so that students might face the empirical, the
visual and the theoretical simultaneously.
We devised two teaching experiments (one using a
Logo microworld and the other Cabri-Géomètre)
during which students worked on activities with the
following structure: first, mathematical objects are
constructed on the computer; second, by attending to the
construction procedure, the properties and relations
underpinning these objects are to be identified and
described; third, the computer resources are used to
generate and test conjectures about further properties and
to inform explanations as to why they must hold; fourth, the
arguments generated during the computer activity are
organised into logical deductive chains in the appropriate
formal language.
Before presenting examples of the students proof
constructions formulated during the experiments, it is
important to stress that, unlike the survey where students
were given the conjectures to be proved, these activities
involved students in both the processes of generating and
proving conjectures. Boero, Garutti and Lemut's (1999)
suggest that students' exploration during these two
processes are similar in nature but differ in function. In
their analysis of the different ways through which students'
generate conditionalities, the central role played by
empirical evidence is clear. The following sections present
some of the ways in which evidence is used in the second
process: the process of proving. These examples are by no
means exhaustive, but have been selected to focus on
different ways in which particular cases were incorporated
in the construction of analytic arguements.
Generic Examples: Using a specific
case to convey a general property
|

Figure 3:
Manipulating to prove
|
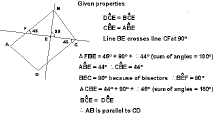
Figure 4:
Calculating to prove
|
Figure 3 presents an attempt to prove that the sum of
five consecutive numbers is always a multiple of five. It
was written by a student who first constructed a variable
Logo procedure to generate a column of n dots, and then used
this to produce a visual representation of the five
consecutive numbers 2, 3, 4, 5 and 6. The student
manipulated the figure in such a way that the conjecture and
its proof emerged simultaneously &endash; in one moment the
student identified both that and why the property holds. No
more examples were deemed to be necessary as there was
nothing special about the choice of 2 for the first number
&endash; or rather what was special about it was that it
represented both the variable n and the first 2 dots in
every column.
The argument presented in Figure 4 shows an
attempt to prove that a quadrilateral in which two
consecutive angle bisectors cross at right angles will have
one set of parallel sides. In common with the previous
argument, one specific case only is included and it was
through manipulations performed on this example that the
student managed to construct his proof. Like the consecutive
numbers example, the student-generated conjecture (that
segment AB is parallel to CD) emerged from the consideration
of just one case. In contrast, the process of determining
why was far from immediate and it was only after
considerable computer exploration that the proof was
attempted. During these investigations, a variety of
configurations of the quadrilateral were created &endash; in
some the given properties were preserved and in others they
were purposefully violated. The first critical moment in the
construction of a proof occurred, ironically, when the
general quadrilateral was turned into a specific case
&endash; that is when the measures for two carefully chosen
(alternate) angles were obtained. From this point on, no
further manipulations of the figure were made. The
calculation of the value 3rd angle in the triangle FBE, a
value which strictly speaking is unnecessary, provided the
second vital step and the obtained value was used as the
basis to deduce the parallel property.
In both these student proofs, the particular
case is presented as a carrier of its underlying
relationships, it serves as a representative for the class
of possible examples. As such, they are both what have been
termed generic examples (Pimm and Mason 1984; Balacheff
1988). Typically, generic examples have been presented as
inferior to arguments formulated in more general terms
(Balacheff, 1988; Harel and Sowder 1998), although Rowland
(1998) has questioned recently whether this pejorative view
is justified. He argues that generic examples provide a
powerful and accessible means of for conviction and
explanation and, at the very least, they might serve as a
"half-way house" between empirical generalisation and
generalised formal proof.
But &endash; apart from the danger that this
brings us back to the hierarchical model of learning that we
wanted to leave behind &endash; what does this mean in
contexts where the distinction between the empirical and the
theoretical is blurred? This is the case in both the
micorworlds we used: A Cabri figure is simultaneous a figure
and a drawing; and working with general Logo procedures also
enables students to experience simultaneously the general
relationships and their specific manifestations. In some
senses, this implies that every Cabri figure and every
instantiation of a general Logo procedure is generic. The
mathematical properties of any particular screen object are
well-known to the student &endash; they received explicit
attention in the construction process. A specific example is
hence one of the possible representations through which an
object can be expressed. The construction process is another
way of expressing of the same object &endash; more tangible
perhaps in the case of Logo, where its symbolic encoding is
easily accessible, than in Cabri. From this perspective it
makes little sense to consider a generic proof as inferior
to a similar argument that happens to be presented using
more general terms.
Constructing a justification from
a special case
|

Figure 5:
An inductive argument
|
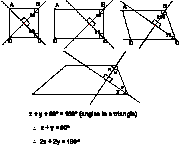
Figure 6:
Special quadrilaterals
|
In contrast to generic examples chosen to be
representative of their class, the examples presented in
Figures 5 and 6 were chosen precisely because of their
specific properties
The argument in Figure 5 shows a another form of
explaining why the sum of five consecutive number is always
a multiple of five. This time, the conjecture was produced
as a result of intensive empirical investigation in which
various sets of five numbers were generated and re-arranged.
In the visual view that emerged from these activities, the
sum of five consecutive number was seen to consist of a
rectanglar block &endash; of width 5 &endash; and a
triangular tail of dots. The proof was constructed using the
reasoning that if the number of dots in the tail is a
multiple of five, than the sum will be too. Testing this
hypothesis involved producing a very particular case, when n
= 0, and then explaining the relationship between this case
and subsequent examples. The proof is hence a visually
inspired example of inductive reasoning, but an inductive
reasoning considerable more developed than that behind the
argument in Figure 2 .
The argument presented in Figure 6 was also
developed from special rather than generic cases. The proof
was constructed in response to the geometry problem
described above, the investigation of properties of a
quadrilateral in which two consecutive bisectors cross at
right angles. It started from the (correct) hypothesis that
a square would satisfy the given properties. Since the
student already knew about various properties of a square,
his next task was to identify which of these properties were
shared by the other quadrilaterals which also satisfied the
givens. He chose to focus on the sum of the two consecutive
angles that had been bisected and, to help in his
explorations, he decided to measure them. Then, he
transformed his square into other well-known cases, a
rectangle, a parallelogram and, finally, a trapezium. He
conjectured that the properties shared by all these
quadrilaterals was that the sum of the two angles is 180(
and his subsequent proof was based on another very familiar
construction, the right-angled triangle. The strategy
employed in the production of this proof is very similar to
that described by Arzarello, Micheletti, Olivero and Robutti
(1998b) and, actually, both the Cabri-inspired proofs
constructed presented in this paper involved what they
describe as abductive as well as deductive reasoning.
The two examples in this section were intended
to illustrate how special cases can form the basis of a
logical argument. Both involve transformations of specific
cases, but the nature of the final proofs was not the same.
The first argument was driven by inductive concerns, a
search for the difference between adjacent cases, while in
the second, finally expressed in a deductive form, the focus
was on identifying the properties shared by the generated
cases. Of course, it could be argued that in the geometry
example, the student did not actually use any specific
examples, but that the square, for example, was general
&endash; the (unknown) measures of the sides of the square
were clearly irrelevant to the activity. This only goes to
show that the distinction between the specific and the
general in the geometry context is far from fixed.
Frameworks for proof?
Up to this point, proof constructions associated with two
different teaching approaches have been considered. In the
first approach, the approach prescribed in the statutory
Mathematics Curriculum for England and Wales, students are
expected to start by experimenting with data and identifying
regularities and only later focus explicitly on mathematical
properties (and later still on the relationships amongst
properties). The second approach involved the use of
computer microworlds in which students construct
mathematical objects in order to provide the data from which
they can abstract further regularities. It has been argued
that the first approach can have the effect of confining
students to empirically based reasoning, while in the second
students engage simultaneously with specific configurations
and general relationships. Even the limited examples
included in this paper illustrate how interacting with the
tools of the Cabri and Logo microworlds can provoke students
to develop a variety of reasoning approaches and facilitate
reflections upon the steps made in constructing and
manipulating new objects. The student proofs presented above
show too how the reflections could be successfully
reorganised into coherent mathematical arguments. Not
surprisingly this did not always happen. One situation in
which all students experienced considerable difficulties was
when the construction of a geometrical object did makes
visible adequate information for a proof &endash; that is
when it was necessary for students to add further
constructions to their figures. This leaves us with a
questions to consider: What activities might help the
student who produced the argument presented in Figure 7
develop the necessary steps to complete the proof?
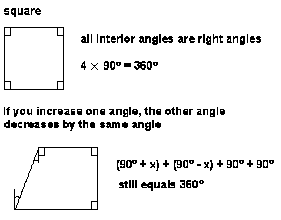
Figure 7:
Where next?
References
Arzarello F., Micheletti C., Olivero
F., Robutti O. (1998a) A model for analysing the
transition to formal proofs in geometry. Proceedings of
the Twenty-second International Conference for the
Psychology of Mathematics Education University of
Stellenbosch, S. Africa. v.2, 24-31.
Arzarello F., Micheletti C., Olivero
F., Robutti O. (1998b) Dragging in Cabri and
Modalities of Transistion from Conjectures to Proofs in
Geometry. Proceedings of the Twenty-second International
Conference for the Psychology of Mathematics
Education University of Stellenbosch, S. Africa.
v.2, 32-39.
Balacheff N. (1988) Une Étude des Processus
de Preuve en Mathématiques, thèse
d'état, Grenoble
Boero P., Garuti R., Lemut E. (1999)
About the Generation of Conditionality of Statements and its
Links with Proving. Proceedings of the Twenty-third
International Conference for the Psychology of Mathematics
Education Haifa, Isreal. v.2, 137-144.
Department for Education (1995) Mathematics in the
National Curriculum London: HMSO
Duval R. (1991). Structure du Raisonnement
Déductif et Apprentissage de la Démonstration.
Educational Studies in Mathematics 22, pp.
233-261.
Duval R. (1998)Geometry from a cognitive point of
view. In: Mammana C., Villani V. (eds) Perspectives on
the Teaching of Geometry for the 21st Century: An ICMI
Study. Kluwer Academic Publishers pp37-51
Harel G., Sowder L. (1998) Students' Proof
Schemes. In E. Dubinsky, A. Schoenfeld, and J. Kaput (Eds.)
Research on Collegiate Mathematics Education. USA:
American Mathematical Society.
Healy L., Hoyles C. (1998) Justifying and
proving in school mathematics: Technical report on
the nationwide survey. Institute of Education, Univ.
London.
Healy L., Hoyles C. (1998) Technical Report
on the Nationwide Survey: Justifying and Proving in School
Mathematics. Institute of Education, University of
London.
Hoyles C., Healy L. (1999) Linking Informal
Argumentation with Formal Proof through Computer-Integrated
Teaching Experiments. In the Proceedings of the
Twenty-third International Conference for the Psychology of
Mathematics Education Haifa, Israel.
Mariotti A., Bartolini Bussi M., Boero
P., Ferri, Garuti R. (1997) Approaching
Geometry Theorems in Context: From History and Epistemolgy
to Cognition. Proceedings of the Twenty-first
International Conference for the Psychology of Mathematics
Education Lahti, Finland v 1. pp 180-195.
Mason J., Pimm D. (1984) Generic Examples:
seeing the General in the Particular. Educational Studies
in Mathematics v. 15 pp. 277-289.
Rowland T. (1998) Conviction, Explanation and Generic
Examples Proceedings of the Twenty-second International
Conference for the Psychology of Mathematics
Education University of Stellenbosch, S. Africa.
v.4, 65-72.
Simon M. A. (1996) Beyond Inductive and Deductive
Reasoning: The Search for a Sense of Knowing. Educational
Studies in Mathematics, 30, pp. 197-210.
|